Problem Statement
Given a 2wire 2701HG-B DSL modem with wireless router connected to the AT&T network and a Netgear N600 Dualband Router WNDR3400. The goal is to connect the two routers into a single network. All machines that are configured to work with the 2wire model should still work once the installation is complete. Ideally, no changes are required to the installed settings in the 2wire router. Both routers should behave like a single network, so regardless of where a device or computer connects, it can see all other devices on the local network. All devices should be able to see the internet regardless of where they connect.
Discussion
WARNING: I am not an network engineer. This discussion and the advice may have issues which result in network security performance issues. This configuration works to the extent it was tested. Use the advice with discretion.
The initial installation consisted of a 2wire 2701HG-B DSL modem with wireless router. This was configured per AT&T instructions using the out-of-the-box installation software. This provided a wireless access point for the internet and local area network capable of about 50Mbps with 4 hard wired access points. The network initially supported b/g wireless connections. Several devices in the home were connected to the network. The setup panels for the 2wire gateway are accessible from http://gateway.2wire.net .
Original Network and Gateway Configuration
A Netgear N600 Dualband Router, model WNDR3400 was obtained for faster local area network access. It supports a/b/g/n wireless access and had two channels so it can devices can connect to either the a/n channel on 5GHz or the b/g/n channel on 2.4 GHz. In an optimal setting, both channels should be capable of 300Mbs. This router also has a USB port which can be configured as network storage: a drive which can be mapped in for use by any device on the network.
There was a fair amount of advice available on how to configure a second router. The key decision is on how the 2nd router should behave. One configuration is to establish a subnet. The 2nd router creates its own local area network which is isolated from the primary router. By opening firewall protections in the 2nd router, misc services like printing and device discover is possible between the primary local area network and the secondary local area network. The key disadvantage to this approach is that if you reconfigure the network in the future, the 2nd router has so many configuration changes it can be difficult to get the network working as expected. Another configuration is to have one router act as a master for the network and services in the other router partially disabled. This is necessary because each router is configured by default to do tasks which will conflict if they are connected together. Specifically, the DHCP services, which assign network addresses to connected devices, can only be performed by one router. So the DHCP services in the second router are disabled so only one router is assigning network addresses.
One last thing is that most routers are themselves devices which require an IP address. So if the second router shares a local area with another router, the IP addresses need to properly configures outside of any automatic address assignments.
The solution works through three network configurations. The first configuration allows devices connected to the second router to see the internet, but the two independent networks exist: devices can only see devices which are connected to the same local area network (LAN). The second configuration partially disables the firewall in the N600. This enables some printers on the primary LAN to be used by devices on the secondary LAN. Finally, both routers are connected together to form a single LAN and all devices can see each other regardless of which router they access.
Solution
Step 1: Configure the N600
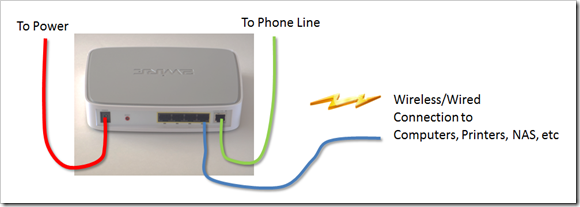
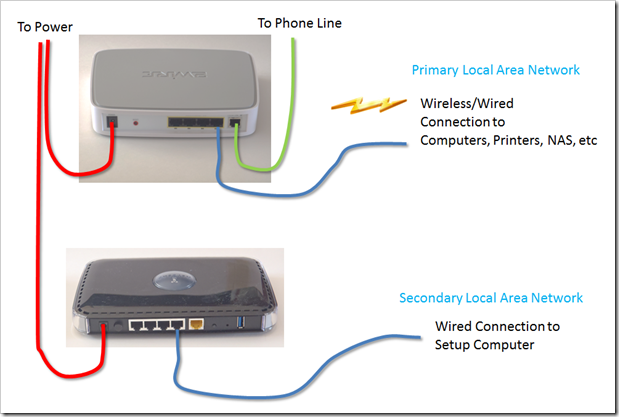
The first step in setting up the network is to install the N600 and configure it. The image below shows how the N600 is wired to the 2wire router. Once this is completed, the computer connected to the N600 is used to configure the N600 using the software disc which was provided. When this is complete, any device connected to the N600 should be able to see the internet through the 2wire gateway. If there is a problem, verify that the internet can be seen by connecting a device to the 2wire gateway. At this step, things like the wireless configuration for the N600 and wireless security can be configured.
Network Setup to configure N600 Router
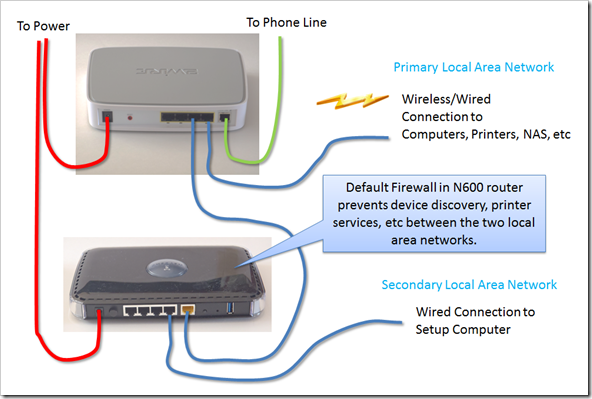
In this configuration, each router assigned IP addresses to the components which connect to it. The firewall in the N600 prevents services like device discovery and printing from working across the network.
At this point, a device connected to the N600 can access the router configurations by connecting to http://www.routerlogin.net. This will bring up the administration page. It can be a good idea to change the admin password to prevent unwanted network changes.
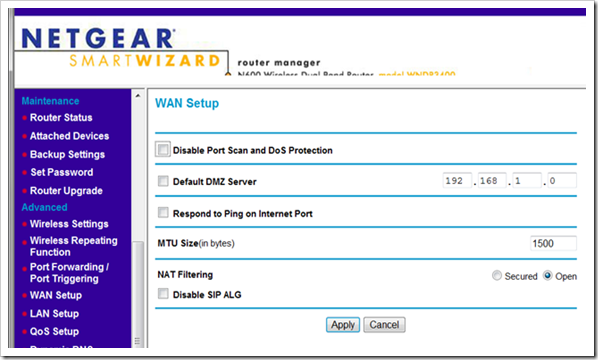
Step 2: Disable NAT Filtering (optional).
With a device connected to the N600, log into the administration pages at http://www.routerlogin.net. On the left had side of the screen, select ‘WAN Setup’. This let you modify what the N600 allows to pass between the two LANs. On the page that appears, set ‘NAT Filtering’ to ‘Open’. Click ‘Apply’ to save the change.
With this change, it should now be possible to access the internet and print to devices connected to the 2wire gateway from devices which are connected to the N600. This configuration can be useable and has a few advantages for situations where high traffic might be present. There are basically two independent networks and the only sharing between them is internet traffic.
Additional changes can probably configure the LAN on the N600 to allow devices on both LANs to see each other, but the testing for that was not done.
Step 3: Reconfigure N600 to share same LAN
This step requires a few things to be done before any testing can be done to confirm the job was done correctly. So there are a few places where things can go wrong.
Step 3a: Identify where the 2wire gateway assigns addresses.
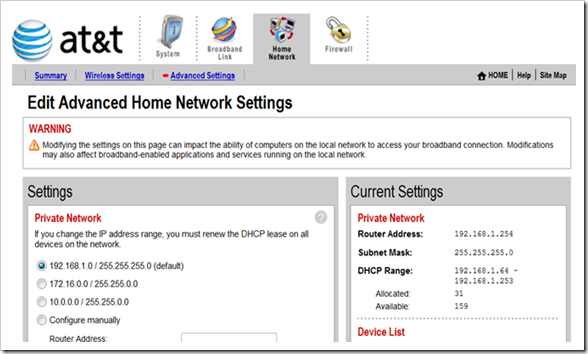
With a device connected to the 2wire gateway, log into http://gateway.2wire.net. Select ‘Home Networking’ and ‘Advanced Settings’. The ‘Private Network’ panel should show where the 2wire gateway assigns IP addresses. In the example below, the base address is 192.168.1.0. By looking at the ‘Current Settings’ the range of assigned addresses can be seen. In this case, the range of assigned addresses are 192.168.1.64 through 192.168.1.253. Keep this range in mind.
Step 3b: Disconnect the N600 from the 2Wire gateway.
Step 3c: Reconfigure the N600.
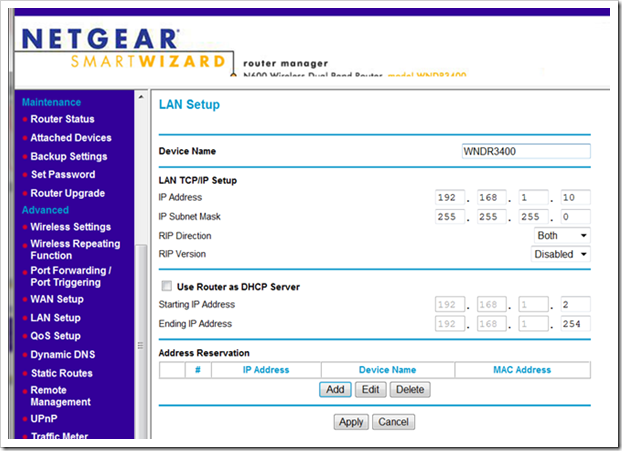
To reconfigure the N600, the DHCP services will be turned off and the IP address of the N600 will be set in address range of the 2wire gateway but outside of the DHCP range for the 2wire gateway. For this system, an address of 192.168.1.10 will work.
With a computer connected to the N600, connect to http://www.routerlogin.net and go to the LAN Setup page. On that page enter 192.168.1.10 as the IP address and unselect ‘Use Router as DHCP Server’. This sets up the address the N600 will appear at in the future and prevents the N600 from assigning network addresses. Click ‘Apply’. The N600 will reset and you may lose communication because the network addresses will no longer be valid. If this happens everything is fine. However you will not be able to do anything with this setup until you do the next step.
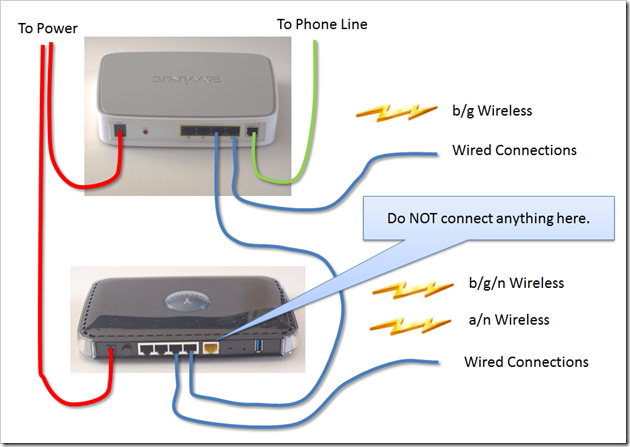
Step 3d: Reconnect the N600 to the 2wire.
Connect one of the LAN ports on the N600 to a LAN port on the 2wire. Do NOT connect anything to the WAN port of the N600. Do NOT use a cross-over cable (If you do not know what this is, do not worry about it).
Step 4: Testing
To test this system, connect a device to the N600. Try to log into the 2wire at http://gateway.2wire.net. If the setup is working, you should be able to log into the 2wire gateway. This proves the N600 and the 2wire are sharing the same LAN. Next log into the N600. Unfortunately, the convenient login address will no longer work since the DHCP services in the N600 were disables. So you have to log in using the IP address: http://192.168.1.10. If you can do this, chances are things are now correctly configured.
Conclusion:
You should have 6 wired ports available (3 on the 2wire, 3 on the N600) and 3 wireless connection options: a b/g wireless connection on the 2wire, a b/g/n connection on the N600, and an a/n connection on the N600. All devices on these connects should be able to see each other and the internet.