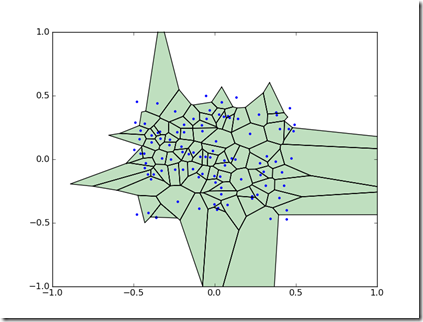
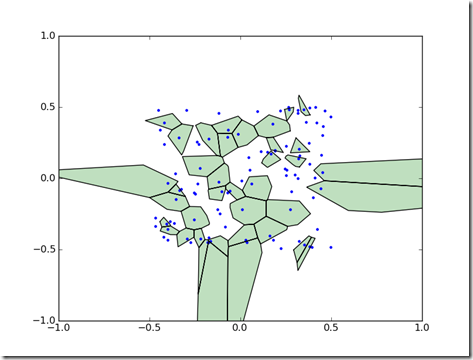
Voronoi diagrams partition a space into cells. Each cell represents the region nearest a point in a set. Voronoi diagrams can be useful for visualizing spatial data.
Qhull is a program which can generate tesselations, convex hulls, and vonoroi diagrams from a set of points. This program is available as a precompiled executable and source code. By interfacing to the command line version of this program, a Voronoi diagram can be generated in Matplotlib.
Sample CodE
To use this code, download Qhull and copy the ‘qvoronoi.exe’ to the working directory. Make sure the code has read, write, and execute privileges in the working directory. Make sure there are not files named ‘data.txt’ or ‘results.txt’ which need to be preserved.
'''
This module generates 2D voronoi diagrams from a list of points.
The vornoi cells can be filtered by supplying a value associated with
each node.
'''
def voronoi2D(xpt,ypt,cpt=None,threshold=0):
'''
This function returns a list of line segments which describe the voronoi
cells formed by the points in zip(xpt,ypt).
If cpt is provided, it identifies which cells should be returned.
The boundary of the cell about (xpt[i],ypt[i]) is returned
if cpt[i]<=threshold.
This function requires qvoronoi.exe in the working directory.
The working directory must have permissions for read and write access.
This function will leave 2 files in the working directory:
data.txt
results.txt
This function will overwrite these files if they already exist.
'''
if cpt is None:
# assign a value to cpt for later use
cpt = [0 for x in xpt]
# write the data file
pts_filename = 'data.txt'
pts_F = open(pts_filename,'w')
pts_F.write('2 # this is a 2-D input set\n')
pts_F.write('%i # number of points\n' % len(xpt))
for i,(x,y) in enumerate(zip(xpt,ypt)):
pts_F.write('%f %f # data point %i\n' % (x,y,i))
pts_F.close()
# trigger the shell command
import subprocess
p = subprocess.Popen('qvoronoi TI data.txt TO results.txt p FN Fv QJ', shell=True)
p.wait()
# open the results file and parse results
results = open('results.txt','r')
# get 'p' results - the vertices of the voronoi diagram
data = results.readline()
voronoi_x_list = []
voronoi_y_list = []
data = results.readline()
for i in range(0,int(data)):
data = results.readline()
xx,yy,dummy = data.split(' ')
voronoi_x_list.append(float(xx))
voronoi_y_list.append(float(yy))
# get 'FN' results - the voronoi edges
data = results.readline()
voronoi_idx_list = []
for i in range(0,int(data)):
data = results.readline()
this_list = data.split(' ')[:-1]
for j in range(len(this_list)):
this_list[j]=int(this_list[j])-1
voronoi_idx_list.append(this_list[1:])
# get 'FV' results - pairs of points which define a voronoi edge
# combine these results to build a complete representation of the
data = results.readline()
voronoi_dict = {}
for i in range(0,int(data)):
data = results.readline().split(' ')
pair_idx_1 = int(data[1])
pair_idx_2 = int(data[2])
vertex_idx_1 = int(data[3])-1
vertex_idx_2 = int(data[4])-1
try:
voronoi_dict[pair_idx_1].append({ 'edge_vertices':[vertex_idx_1,vertex_idx_2],
'neighbor': pair_idx_2 })
except KeyError:
voronoi_dict[pair_idx_1] = [{ 'edge_vertices':[vertex_idx_1,vertex_idx_2],
'neighbor': pair_idx_2 } ]
try:
voronoi_dict[pair_idx_2].append({ 'edge_vertices':[vertex_idx_1,vertex_idx_2],
'neighbor': pair_idx_1 })
except KeyError:
voronoi_dict[pair_idx_2] = [{ 'edge_vertices':[vertex_idx_1,vertex_idx_2],
'neighbor': pair_idx_1 } ]
#################
# generate a collection of voronoi cells
x_list = []
y_list = []
for point_idx in voronoi_dict.keys():
if cpt[point_idx]<=threshold:
# display this cell, so add the data to the edge list
e_list = []
for edge in voronoi_dict[point_idx]:
p1_idx = edge['edge_vertices'][0]
p2_idx = edge['edge_vertices'][1]
e_list.append((p1_idx,p2_idx))
# put the vertices points in order so they
# walk around the voronoi cells
p_list = [p1_idx]
while True:
p=p_list[-1]
for e in e_list:
if p==e[0]:
next_p = e[1]
break
elif p==e[1]:
next_p = e[0]
break
p_list.append(next_p)
e_list.remove(e)
if p_list[0]==p_list[-1]:
# the cell is closed
break
# build point list
if all([p>=0 for p in p_list]):
for p in p_list:
if p>=0:
x_list.append(voronoi_x_list[p])
y_list.append(voronoi_y_list[p])
x_list.append(None)
y_list.append(None)
return (x_list,y_list)
if __name__=='__main__':
import random
xpt = [random.random()-0.5 for i in range(0,100)]
ypt = [random.random()-0.5 for i in range(0,100)]
cpt = [random.random()-0.5 for i in range(0,100)]
(x_list,y_list) = voronoi2D(xpt,ypt,cpt)
import matplotlib.pyplot as pp
pp.figure()
pp.plot(xpt,ypt,'b.')
pp.plot(x_list,y_list,'k-')
pp.fill(x_list,y_list,'g',alpha=0.25,edgecolor='none')
pp.axis([-1,1,-1,1])
pp.show()
When run, this module will produce a Voronoi diagram with the cells which have a value greater than zero visible.