Figure 1
Problem Statement:
Can using OpenCL with Python significantly improve the performance of the Ellipse Fit problem? This problem was introduced here and improved on here using vectorization, and here using parallelization.
Discussion:
OpenCL is an open, royalty free, cross platform standard for parallel programming on heterogeneous systems. PyOpenCL is a wrapper for OpenCL which allows blending an OpenCL program into a Python script. PyOpenCL requires some setup to incorporate into a script. Any OpenCL program must be configured to work with a Python script. In general, a text representation of the OpenCL function (work task) is created. The device which will execute the program needs to be selected. The function needs to have input and output buffers defined to move data between the main program and the device which will execute the work task. Before the work task is called, the input buffers must be filled with data. The text representation of the work task must be compiled before execution. Finally, the function is called and it loads data into the output buffers when it completes.
One advantage of OpenCL is the ability to move a program among different devices for execution. One of the disadvantages is that there are multiple tuning aspects to tune which can affect performance. The best configuration for one device is usually not optimal for other devices.
Testing Setup:
To recreate these experiments, recreate the test setup here, then add the objective function from here. Then add the new function objective_openCL.py. Finally, overwrite the main.py script with the one here.
objective_openCL.py
'''
This module contains an objective function for the ellipse fitting problem.
The objective is coded using vectorized operations.
'''
from numpy import *
import pyopencl as cl
from string import Template
# local imports
import objective_scalar
class Objective(objective_scalar.Objective):
def __init__(self,parameters):
objective_scalar.Objective.__init__(self,parameters)
precision_dict = {
'float':float32,
'double':float64}
self.platform_name = parameters.get('platform_name',None)
self.platform_precision = parameters.get('platform_precision','double')
self.partial_sum_loc = parameters.get('partial_sum_loc','__global')
self.numpy_prec = precision_dict[self.platform_precision]
openCL_prec = self.platform_precision
point_list = self._p
x,y = zip(*point_list)
self.x = array(x,dtype=self.numpy_prec)
self.y = array(y,dtype=self.numpy_prec)
self.f1 = array([0,0],copy=True,dtype=self.numpy_prec)
self.f2 = array([0,0],copy=True,dtype=self.numpy_prec)
self.a = array([0],copy=True,dtype=self.numpy_prec)
self.num_elements = len(x)
platforms = cl.get_platforms()
if len(platforms)>1 and not self.platform_name is None:
# select the the first device in list
for platform in platforms:
if self.platform_name in platform.name:
# use first device for context
for device in platform.get_devices():
self.ctx = cl.Context([device])
self.device = device
break
break
else:
self.ctx = cl.create_some_context()
if 'NVIDIA' in self.platform_name:
compiler_options = '-cl-mad-enable -cl-fast-relaxed-math'
else:
compiler_options = ''
#self.ctx = cl.create_some_context()
self.queue = cl.CommandQueue(self.ctx)
# define the input buffers and transfer data into them
mf = cl.mem_flags
self.x_buf = cl.Buffer(self.ctx, mf.READ_ONLY | mf.COPY_HOST_PTR, hostbuf=self.x)
self.y_buf = cl.Buffer(self.ctx, mf.READ_ONLY | mf.COPY_HOST_PTR, hostbuf=self.y)
self.f1_buf = cl.Buffer(self.ctx, mf.READ_ONLY | mf.COPY_HOST_PTR, hostbuf=self.f1)
self.f2_buf = cl.Buffer(self.ctx, mf.READ_ONLY | mf.COPY_HOST_PTR, hostbuf=self.f2)
self.a_buf = cl.Buffer(self.ctx, mf.READ_ONLY | mf.COPY_HOST_PTR, hostbuf=self.a)
# define the output buffer
self.partial_sum_buf = cl.Buffer(self.ctx, mf.READ_WRITE, self.x.nbytes)
self.full_sum_buf = cl.Buffer(self.ctx, mf.READ_ONLY, array([0],dtype=self.numpy_prec).nbytes)
# prep the container to the output
self.partial_sum = empty(self.x.shape,dtype=self.numpy_prec)
self.full_sum = empty(array([0],dtype=self.numpy_prec).shape,dtype=self.numpy_prec)
# define local memory if needed
if not self.partial_sum_loc=='__global':
self.local_partial_sum = cl.LocalMemory(self.x.nbytes)
code_pattern= Template("""
#pragma OPENCL EXTENSION cl_khr_fp64: enable
__kernel void partial_sum(
__global const ${precision} *x,
__global const ${precision} *y,
__global const ${precision} *f1,
__global const ${precision} *f2,
__global const ${precision} *a,
${partial_sum_loc} ${precision} *partial_sum)
{
int gid = get_global_id(0);
${precision} x_f1_diff = x[gid]-f1[0];
${precision} x_f2_diff = x[gid]-f2[0];
${precision} y_f1_diff = y[gid]-f1[1];
${precision} y_f2_diff = y[gid]-f2[1];
${precision} x_f1_diff_sq = x_f1_diff*x_f1_diff;
${precision} x_f2_diff_sq = x_f2_diff*x_f2_diff;
${precision} y_f1_diff_sq = y_f1_diff*y_f1_diff;
${precision} y_f2_diff_sq = y_f2_diff*y_f2_diff;
${precision} norm_pt_to_f1 = sqrt(x_f1_diff_sq+y_f1_diff_sq);
${precision} norm_pt_to_f2 = sqrt(x_f2_diff_sq+y_f2_diff_sq);
${precision} t1 = norm_pt_to_f1+norm_pt_to_f2-2*a[0];
partial_sum[gid]=t1*t1;
}
__kernel void full_sum(
${partial_sum_loc} ${precision} *partial_sum,
__global ${precision} *full_sum)
{
long i;
${precision} sum=0;
for(i=0; i<${num_elements}; i++) {
sum += partial_sum[i];
}
full_sum[0] = sum;
}
__kernel void full_sum2(
__global ${precision} *partial_sum)
{
int gid = get_global_id(0);
long i;
long mid_point = (${num_elements}+1)/2;
if (gid>mid_point) {
return;
} else {
partial_sum[gid]+=partial_sum[gid+mid_point];
}
}
""")
substitutions = {'precision':openCL_prec,
'num_elements':self.num_elements,
'partial_sum_loc':self.partial_sum_loc}
prg = code_pattern.substitute(substitutions)
# define the function to be executed
self.prg = cl.Program(self.ctx, prg).build(options=compiler_options)
def __call__(self,x):
'''
Calculate the objective cost in the optimization problem.
'''
a = x[0]
self.a = array([x[0]],copy=False,dtype=self.numpy_prec)
self.f1 = array([x[1],x[2]],copy=False,dtype=self.numpy_prec)
self.f2 = array([x[3],x[4]],copy=False,dtype=self.numpy_prec)
# trigger transfer of values to the GPU buffers
# only those values which changed before this evaluation need to be updated
mf = cl.mem_flags
self.f1_buf = cl.Buffer(self.ctx, mf.READ_ONLY | mf.COPY_HOST_PTR, hostbuf=self.f1)
self.f2_buf = cl.Buffer(self.ctx, mf.READ_ONLY | mf.COPY_HOST_PTR, hostbuf=self.f2)
self.a_buf = cl.Buffer(self.ctx, mf.READ_ONLY | mf.COPY_HOST_PTR, hostbuf=self.a)
# execute the partial_sum function
if self.partial_sum_loc == '__global':
self.prg.partial_sum(self.queue, self.x.shape, None,
self.x_buf,self.y_buf,self.f1_buf,self.f2_buf,self.a_buf,self.partial_sum_buf)
# trigger the copy of the results into the partial_sum container after completion
cl.enqueue_read_buffer(self.queue, self.partial_sum_buf, self.partial_sum).wait()
# execute the full_sum function
self.prg.full_sum(self.queue, (1,), None,
self.partial_sum_buf,self.full_sum_buf)
else:
self.prg.partial_sum(self.queue, self.x.shape, (8,),
self.x_buf,self.y_buf,self.f1_buf,self.f2_buf,
self.a_buf,self.local_partial_sum)
self.prg.full_sum(self.queue, (1,), None,
self.local_partial_sum,self.full_sum_buf)
# trigger the copy of the results into the partial_sum container after completion
cl.enqueue_read_buffer(self.queue, self.full_sum_buf, self.full_sum).wait()
# compare sums
#print (sum(self.full_sum)-sum(self.partial_sum))
#print (sum(self.full_sum),sum(self.partial_sum))
# finish up the calculations
point_list = self._p
n = float(len(point_list))
_lambda =0.1
#full_sum = sum(self.partial_sum)
total = (self.full_sum/float(n) +
_lambda*self._ahat_max*self._sigma*exp((a/self._ahat_max)**4))
return total
def _del_(self):
pass
if __name__=='__main__':
import time
from random import uniform,normalvariate,seed
# local modules
import ellipse
####################################################################
# setup test conditions
num_reps = 1
num_pts = 1e6
precision = 'float'
seed(1234567890) # set the random generator to get repeatable results
# setup the reference ellipse
# define the foci locations
foci1_ref = array([2,-1])
foci2_ref = array([-2,1])
# define distance from foci to ellipse circumference
a_ref = 2.5
point_list = ellipse.generate_point_list(num_pts,a_ref,foci1_ref,foci2_ref)
parameters = { "point_list" : point_list,
"platform_name" : 'NVIDIA',
"platform_precisions" : precision}
# test the function on an NVIDIA card
t0 = time.time()
my_objective = Objective(parameters)
x = my_objective.x0
t1 = time.time()
for i in range(0,num_reps):
y = my_objective(x)
t2 = time.time()
print ''
print 'NVIDIA initialization took %f sec' % (t1-t0)
print 'NVIDIA execution took %f sec' % (t2-t1)
print 'Executed %i times on %s' % (num_reps,my_objective.device.name)
print ''
# test the function on an intel CPU
parameters = { "point_list" : point_list,
"platform_name" : 'Intel',
"platform_precisions" : precision}
t0 = time.time()
my_objective = Objective(parameters)
x = my_objective.x0
t1 = time.time()
for i in range(0,num_reps):
y = my_objective(x)
t2 = time.time()
print ''
print 'Intel initialization took %f sec' % (t1-t0)
print 'Intel execution took %f sec' % (t2-t1)
print 'Executed %i times on %s' % (num_reps,my_objective.device.name)
print ''
main.py
'''
This module tests the performance of different ways of
forming the ellipse fit objective function and
its impact on the ellipse fit optimization
problem.
'''
__author__ = 'Ed Tate'
__email__ = 'edtate<at>gmail-dot-com'
__website__ = 'exnumerus.blogspot.com'
__license__ = 'Creative Commons Attribute By - http://creativecommons.org/licenses/by/3.0/us/'''
import time
from random import uniform, normalvariate, seed
from numpy import *
import pylab as plt
from openopt import NLP
import gc
# local modules
import ellipse
import objective_scalar
import objective_vectorized
import objective_vectorized_parallel
import objective_openCL
####################################################################
# setup test conditions
num_reps = 2
seed(1234567890) # set the random generator to get repeatable results
# setup the reference ellipse
# define the foci locations
foci1_ref = array([2,-1])
foci2_ref = array([-2,1])
# define distance from foci to ellipse circumference
a_ref = 2.5
######################################################
# setup the OpenCL Objective classes for CPU and GPU verions of the
# OpenCL version of the objective function
class objective_openCL_GPU_Objective(objective_openCL.Objective):
def __init__(self,parameters):
parameters["platform_name"]="NVIDIA"
objective_openCL.Objective.__init__(self,parameters)
class objective_openCL_CPU_Objective(objective_openCL.Objective):
def __init__(self,parameters):
parameters["platform_name"]="Intel"
objective_openCL.Objective.__init__(self,parameters)
#####################################################
#
objective_functions = [objective_scalar.Objective,
objective_vectorized.Objective,
objective_vectorized_parallel.Objective,
objective_openCL_GPU_Objective,
objective_openCL_CPU_Objective]
legends = ['scalar','vectorized','vectorized parallel',
'OpenCL on NVIDIA GPU',
'OpenCL on Intel i7 CPU']
######################################################
# measure the timing to setup and call the objective function
num_pts_list = [10,100,250,500,1000,2500,5000,10000,50000,1e5,1e6]
#num_pts_list = [10,100,250]
setup_times = []
call_times = []
for num_pts in num_pts_list:
seed(1234567890) # set the random generator to get repeatable results
point_list = ellipse.generate_point_list(num_pts,a_ref,foci1_ref,foci2_ref)
parameters = { "point_list" : point_list }
test_setup_times = []
test_call_times = []
for objective_function in objective_functions:
t0 = time.time()
my_objective = objective_function(parameters)
x0 = my_objective.x0
t1 = time.time()
for i in range(0,num_reps):
y = my_objective(x0)
t2 = time.time()
test_setup_times.append(t1-t0)
test_call_times.append(t2-t1)
del my_objective
setup_times.append(test_setup_times)
call_times.append(test_call_times)
print 'Evaluated %i points' % num_pts
# plot the results
plt.figure()
plt.loglog(num_pts_list,call_times,lw=2)
plt.legend(legends,loc='upper left')
plt.xlabel('Number of points')
plt.ylabel('Execution Time [sec]')
plt.title('Times for %i calls to objective function' % num_reps)
plt.grid(True)
#############################################################
# test the performance when used in an optimizer
num_pts_list = [10,100,250,500,1000,2500,5000]
#num_pts_list = [10,100,250]
setup_times = []
call_times = []
for num_pts in num_pts_list:
seed(1234567890) # set the random generator to get repeatable results
point_list = ellipse.generate_point_list(num_pts,a_ref,foci1_ref,foci2_ref)
parameters = { "point_list" : point_list }
test_setup_times = []
test_call_times = []
for objective_function in objective_functions:
t0 = time.time()
my_objective = objective_function(parameters)
x0 = my_objective.x0
p_vectorized = NLP(my_objective, x0, iprint = -1)
t1 = time.time()
opt_result = p_vectorized.solve('ralg')
t2 = time.time()
test_setup_times.append(t1-t0)
test_call_times.append(t2-t1)
print '%s : %s' % (opt_result.xf,objective_function)
del my_objective
gc.collect() # force release of resources held by the objective
setup_times.append(test_setup_times)
call_times.append(test_call_times)
print 'Evaluated %i points' % num_pts
print
# plot the results
plt.figure()
plt.loglog(num_pts_list,call_times,lw=2)
plt.legend(legends,loc='upper left')
plt.xlabel('Number of points')
plt.ylabel('Execution Time [sec]')
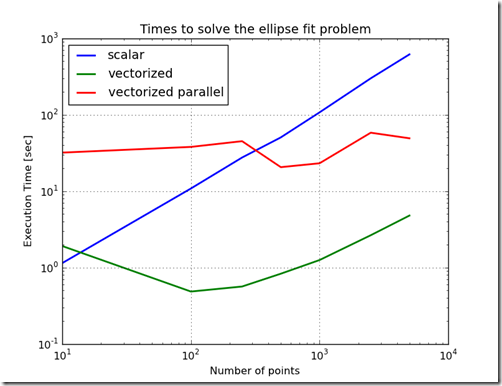
plt.title('Times to solve the ellipse fit problem')
plt.grid(True)
plt.show()
Testing results:
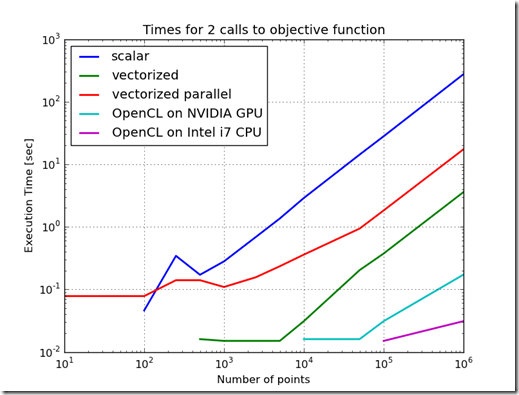
Figure 1 shows the difference in time to call the objective function for the various methods of implementing the objective function. From this chart, the worst performing method is to implement the objective function as a scalar. The best performing implementation is to implement the function using OpenCL on the CPU. This variation in performance is not as stark when the objective function is used in the Ellipse Fit problem. In fact, because the ellipse fit problem measures data transfer times and computation times, the ordering of the performance changes. When just measuring the time to evaluate the objective function, the increasing order of performance is scalar, parallelized & vectorized, vectorized, OpenCL on GPU, and the best performance is OpenCL on the CPU. Furthermore, as the problem scale changed, the relative performance ratios stay relatively constant.When the ellipse fit problem is solved, the ordering changes and the relative slopes change. One reason for this is the overhead associated with the optimization routines. Another reason is the increased time which includes time to transfer data into the GPU. Another interesting result is that the execution times do not change much as the problem size increases. This is probably due to the efficiency of the computation and the efficiency of block transfers of data.
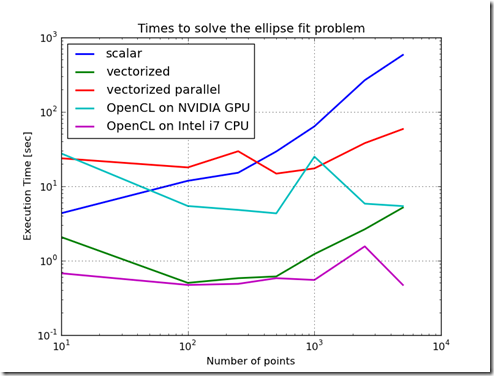
Figure 2
One other thing to note is that these different methods of computation have different resolutions in the floating point numbers. Because of these differences in the resolution, the optimization problem finds slightly different answers. The console output shows the differences in the results of the optimization. In general, for the larger problems, the difference are about one part in 10,0000.
Console Output:
Evaluated 10 points
Evaluated 100 points
Evaluated 250 points
Evaluated 500 points
Evaluated 1000 points
Evaluated 2500 points
Evaluated 5000 points
Evaluated 10000 points
Evaluated 50000 points
Evaluated 100000 points
Evaluated 1000000 points
[ 2.53977781 -1.9791083 1.11795369 1.90068376 -0.97398384] : <class 'objective_scalar.Objective'>
[ 2.53978396 -1.97911311 1.11797418 1.90068553 -0.97399285] : <class 'objective_vectorized.Objective'>
[ 2.53980864 -1.9791325 1.11805566 1.90069183 -0.97402764] : <class 'objective_vectorized_parallel.Objective'>
[ 2.53972748 -1.97906577 1.1177896 1.90067428 -0.9739137 ] : <class '__main__.objective_openCL_GPU_Objective'>
[ 2.53977167 -1.97910332 1.11793354 1.90068234 -0.97397521] : <class '__main__.objective_openCL_CPU_Objective'>
Evaluated 10 points
[ 2.566147 -1.95135142 1.0549304 2.16680656 -1.10160299] : <class 'objective_scalar.Objective'>
[ 2.56614697 -1.95134842 1.05492776 2.16681334 -1.10160238] : <class 'objective_vectorized.Objective'>
[ 2.56614691 -1.95134982 1.05492914 2.16680969 -1.1016027 ] : <class 'objective_vectorized_parallel.Objective'>
[ 2.56614661 -1.95134401 1.05492394 2.16682259 -1.10160128] : <class '__main__.objective_openCL_GPU_Objective'>
[ 2.56614672 -1.95134937 1.05492891 2.16680991 -1.10160258] : <class '__main__.objective_openCL_CPU_Objective'>
Evaluated 100 points
[ 2.56330383 -2.0896741 1.06288154 2.04214077 -1.05030978] : <class 'objective_scalar.Objective'>
[ 2.5633038 -2.08967399 1.06288158 2.04214065 -1.05031 ] : <class 'objective_vectorized.Objective'>
[ 2.56330231 -2.08967161 1.06288221 2.04213788 -1.05031417] : <class 'objective_vectorized_parallel.Objective'>
[ 2.56330174 -2.08967069 1.0628825 2.04213675 -1.05031584] : <class '__main__.objective_openCL_GPU_Objective'>
[ 2.56330119 -2.08966978 1.0628827 2.04213573 -1.05031742] : <class '__main__.objective_openCL_CPU_Objective'>
Evaluated 250 points
[ 2.55213105 -2.06212704 1.05749405 2.02108216 -1.05369719] : <class 'objective_scalar.Objective'>
[ 2.55390449 -2.0623902 1.05823288 2.02404738 -1.05682491] : <class 'objective_vectorized.Objective'>
[ 2.54907192 -2.05769363 1.05956421 2.01575473 -1.05475975] : <class 'objective_vectorized_parallel.Objective'>
[ 2.55212491 -2.06209759 1.05747762 2.02105559 -1.05370312] : <class '__main__.objective_openCL_GPU_Objective'>
[ 2.5518505 -2.06217932 1.05803857 2.02239691 -1.05392966] : <class '__main__.objective_openCL_CPU_Objective'>
Evaluated 500 points
[ 2.61796899 -2.14539556 1.11170214 2.12027043 -1.09253186] : <class 'objective_scalar.Objective'>
[ 2.61708437 -2.14479931 1.10835605 2.12087692 -1.090721 ] : <class 'objective_vectorized.Objective'>
[ 2.61761133 -2.14669529 1.1089428 2.12139812 -1.09022015] : <class 'objective_vectorized_parallel.Objective'>
[ 2.61753131 -2.14662822 1.10869732 2.12152618 -1.09010436] : <class '__main__.objective_openCL_GPU_Objective'>
[ 2.61763094 -2.14672541 1.10895434 2.12136288 -1.09017078] : <class '__main__.objective_openCL_CPU_Objective'>
Evaluated 1000 points
[ 2.60471429 -2.11563461 1.06998647 2.13374471 -1.0697982 ] : <class 'objective_scalar.Objective'>
[ 2.60416974 -2.11432462 1.07083334 2.13291023 -1.07026969] : <class 'objective_vectorized.Objective'>
[ 2.60416139 -2.1136674 1.0722599 2.13226116 -1.07119697] : <class 'objective_vectorized_parallel.Objective'>
[ 2.60527276 -2.11598152 1.07174066 2.13404717 -1.07158798] : <class '__main__.objective_openCL_GPU_Objective'>
[ 2.60428855 -2.11418258 1.07163536 2.13309981 -1.07148272] : <class '__main__.objective_openCL_CPU_Objective'>
Evaluated 2500 points
[ 2.65236805 -2.17113736 1.11832436 2.18090649 -1.10477807] : <class 'objective_scalar.Objective'>
[ 2.65236757 -2.17113597 1.11832359 2.18090679 -1.10477991] : <class 'objective_vectorized.Objective'>
[ 2.65236655 -2.1711387 1.1183202 2.18090519 -1.10477049] : <class 'objective_vectorized_parallel.Objective'>
[ 2.65124389 -2.17148832 1.11786432 2.17945815 -1.10311976] : <class '__main__.objective_openCL_GPU_Objective'>
[ 2.65124383 -2.17148872 1.11786446 2.17945781 -1.10311962] : <class '__main__.objective_openCL_CPU_Objective'>
Evaluated 5000 points
Conclusions:
- Using PyOpenCl is significantly faster then Numpy in this problem when using the CPU or the GPU to perform the calculation. The OpenCL version of the objective function solved on the GPU was over 10 times faster than the Numpy version of the objective function. The OpenCL version solved on the CPU was almost 100 times faster then the Numpy version.
- The OpenCL version of the objective function was able to be redirected from the the GPU to the CPU using a a single line of code.
- Using the native CPU with OpenCL is significantly faster then using the GPU for this problem. For this problem, the performance difference is related to the fact that the computational load is roughly proportional the quantity of data which is transferred into the device. When the OpenCL program executes on the CPU, the data transfer times are very low. When the OpenCL program runs on the GPU, global memory is used, which requires a data transfer from the CPU’s memory space to the GPU memory space. This is usually relatively slow.
- Because of the differences in the numeric representation of the floating point values, the OpenCL calculations introduce differences in the calculations compared to the scalar, the Numpy, and parallelized Numpy representations.
Hardware Configuration:
- Pythonxy 2.6.6
- PyOpenCL 0.92
- Sony Vaio VPCF1
- Intel i7 Q740 @ 1.73 GHz
- NVIDIA GeForce GT 425M @ 1.12 GHz
References:
- Khronos Group OpenCL Standard
- NVIDIA OpenCL manuals
- Intel OpenCL manuals
- PyOpenCL Home Page
- PyOpenCL Documents





![ExampleEllipse[4] ExampleEllipse[4]](http://lh4.ggpht.com/-0N0KJxjuMGo/TfL-MJv5wsI/AAAAAAAAARw/9R8xuBHmw4o/ExampleEllipse%25255B4%25255D_thumb%25255B1%25255D.png?imgmax=800)