One nice property of the Astar algorithm is that if a finite path exists between two nodes on an infinite order graph, and a good heuristic is chosen, then the Astar algorithm can find the shortest path with finite resources. One of the challenges is representing an infinite order graph in finite resources. Another challenge is making sure the heuristic is reasonable. However once those two issues are adequately addressed, searching for a shortest path on an infinite order graph can be done.
Wednesday, October 20, 2010
Sunday, October 10, 2010
Finding the shortest path between two points: An example of the A* algorithm in Python
Introduction:
One common challenge is finding the shortest or least expensive path between two points. This simple problem can represent many different engineering and information processing problems. One of the most familiar versions of this problem is finding the shortest or fastest way to travel through between two points on a map.A famous variant of this problem is the traveling salesman problem. To set up this kind of problem, a directed graph needs to be created. A directed graph defines the connection between nodes. It also defines the cost to travel between nodes.
Given an origin and a destination in the graph, there are many ways to find the shortest path (or least cost) path between the origin and destination. One way which is usually intractable is to do a brute force search. However, of the tractable ways to solve the problem, the A* algorithm can be fast and efficient if a few conditions are met: an approximate estimate of the cost to reach the destination from every point in the graph is available and this approximation is always equal to or less than the optimal cost to reach the destination.
An Example Problem:
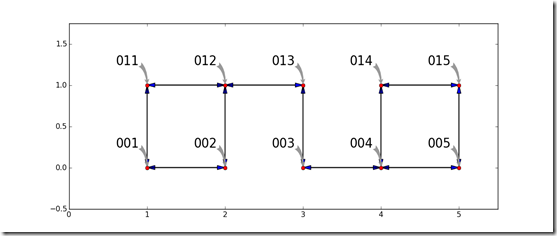
A shortest path problem has the goal of finding a path through a graph which costs the least. Consider the simple graph shown below. Each node is represented by a red circle. The ways to travel between the nodes (the edges, arcs, arrows, etc) are shown by arrows between the nodes. each node has a name which is called out. To make the graph interesting, there is no way to travel in one step between the pair of nodes in 002 and 003 and the other pair of 013 and 014. To keep the problem simple, the cost to travel on every edge is equal to the Euclidean distance along the edge.
The Astar algorithm can find a route from an origin to a destination node. For this example, the goal is to find a minimum cost route from node 001 to node 015. The graph is stored as a dictionary which has an entry for each node. This entry has a dictionary which defined the x and y coordinates of the node along with a list of nodes which can be reached. Furthermore, the approximate cost from each node to the destination is defined as the Euclidean distance from a given node to the destination. This distance satisfies the requirements for a good approximation in this model because it will always be equal or less than the best distance that can be achieved following the edges.
This implementation of the Astar algorithm is almost identical to the algorithm outlined in Wikipedia.
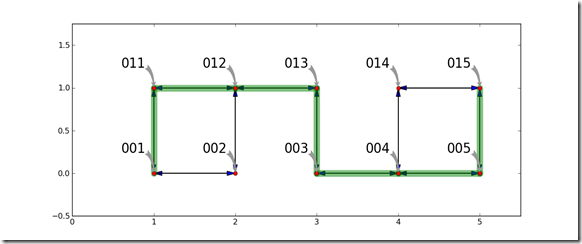
Once the Astar algorithm solves for the shortest path, the shortest path is visualized by laying it on top of the graph.
One key result can easily be seen in this example. By looking carefully at the graph, it should be obvious that there are other routes which can travel between the origin and destination with the same distance or cost. For some problems, there is not a single shortest path, there are potentially many paths which have the same cost. This algorithm will generate only one. There may be other routes which are the shortest path.
Code Example:
def Astar(start,goal,dist_between,neighbor_nodes,heuristic_estimate_of_dist):
closedset = set([]) # The set of nodes already evaluated.
openset = set([start]) # The set of tentative nodes to be evaluated.
# starts off containing initial node
came_from = set([]) # The map of navigated nodes.
g_score={start:0} # Distance from start along optimal path.
h_score={start:heuristic_estimate_of_dist(start,goal)}
f_score={start:h_score[start]} #Estimated total distance from start to goal through y.
came_from={start:None}
while len(openset)>0: # open set is not empty
#x := the node in openset having the lowest f_score[] value
bestX = None
for x in openset:
if bestX==None:
bestX = x
elif f_score[x] < f_score[bestX]:
bestX = x
x = bestX
if x == goal:
return reconstruct_path(came_from,came_from[goal])
openset.discard(x)
closedset.add(x)
neighbor_list = neighbor_nodes(x)
for y in neighbor_nodes(x):
if y in closedset:
continue
tentative_g_score = g_score[x] + dist_between(x,y)
if y not in openset:
openset.add(y)
tentative_is_better = True
elif tentative_g_score < g_score[y]:
tentative_is_better = True
else:
tentative_is_better = False
if tentative_is_better == True:
came_from[y] = x
g_score[y] = tentative_g_score
h_score[y] = heuristic_estimate_of_dist(y, goal)
f_score[y] = g_score[y] + h_score[y]
return None
def reconstruct_path(came_from, current_node):
if not came_from[current_node] == None:
p = reconstruct_path(came_from, came_from[current_node])
return (p + [current_node])
else:
return [current_node]
#####################################
if __name__=='__main__':
import pylab as p
graph = {
'001':dict(x=1, y=0,nextList=['002','011']),
# '002':dict(x=2, y=0,nextList=['001','003','012']),
# '003':dict(x=3, y=0,nextList=['002','004','013']),
'002':dict(x=2, y=0,nextList=['001','012']),
'003':dict(x=3, y=0,nextList=['004','013']),
'004':dict(x=4, y=0,nextList=['003','005','014']),
'005':dict(x=5, y=0,nextList=['004','015']),
'011':dict(x=1, y=1,nextList=['012','001']),
'012':dict(x=2, y=1,nextList=['011','013','002']),
# '013':dict(x=3, y=1,nextList=['012','014','003']),
# '014':dict(x=4, y=1,nextList=['013','015','004']),
'013':dict(x=3, y=1,nextList=['012','003']),
'014':dict(x=4, y=1,nextList=['015','004']),
'015':dict(x=5, y=1,nextList=['014','005']),
}
def neighbor_nodes(x):
return graph[x]['nextList']
def distance_between(x,y):
_x1 = graph[x]['x']
_x2 = graph[y]['x']
_y1 = graph[x]['y']
_y2 = graph[y]['y']
return ((_x1-_x2)**2+(_y1-_y2)**2)**(0.5)
def drawArrow(xFrom,xTo,yFrom,yTo):
length = ((xFrom-xTo)**2+(yFrom-yTo)**2)**(0.5)
head_len = 0.1
head_width = 0.05
dx = ((length-head_len)/length)*(xTo-xFrom)
dy = ((length-head_len)/length)*(yTo-yFrom)
p.arrow(xFrom,yFrom,dx,dy,
head_width=head_width,head_length=head_len)
def plotGraph(graph,ax):
first = True
for origin in graph.keys():
for dest in graph[origin]['nextList']:
xFrom = graph[origin]['x']
xTo = graph[dest]['x']
yFrom = graph[origin]['y']
yTo = graph[dest]['y']
drawArrow(xFrom,xTo,yFrom,yTo)
if first:
minX = xFrom
maxX = xFrom
minY = yFrom
maxY = yFrom
first = False
else:
minX = min(minX,xFrom)
maxX = max(maxX,xFrom)
minY = min(minY,yFrom)
maxY = max(maxY,yFrom)
p.plot([xFrom],[yFrom],'or')
ax.annotate(origin, xy=(xFrom,yFrom), xycoords='data',
xytext=(-50, 30), textcoords='offset points',
size=20,
#bbox=dict(boxstyle="round", fc="0.8"),
arrowprops=dict(arrowstyle="fancy",
fc="0.6", ec="none",
# patchB=el,
connectionstyle="angle3,angleA=0,angleB=-90"),
)
#p.axis([minX-0.25,maxX+0.25,minY-0.25,maxY+0.25])
def plotRoute(route,graph):
for idx,point in enumerate(route):
if idx < len(route)-1:
nextPoint = route[idx+1]
xFrom = graph[point]['x']
xTo = graph[nextPoint]['x']
yFrom = graph[point]['y']
yTo = graph[nextPoint]['y']
p.plot([xFrom,xTo],[yFrom,yTo],'-g',lw=10,alpha=0.5,solid_capstyle='round')
fig = p.figure()
ax = fig.add_subplot(111, autoscale_on=False, xlim=(0,5.5), ylim=(-0.5,1.75))
route = Astar('001','015',distance_between,neighbor_nodes,distance_between)
route.append('015')
print route
plotRoute(route,graph)
plotGraph(graph,ax)
print 'Done'
p.show()
References:
Tuesday, October 5, 2010
Beta release: How to render OpenStreetMaps using Python and Matplotlib
Introduction:
Open Street Maps is an collaboratively developed and open source map database. The entire OSM database or specific portions can be downloaded. The database includes information on roads, political boundaries, natural features, rail lines, trails, and much more. The website can generate output files with sufficient information to create custom and detailed surface street maps for many areas of the world. With Python and Matplotlib the XML data in an OpenStreetMaps OSM file can be rendered as a custom map can be rendered to meet specific needs. Below is an example of a map which can be generated from and OSM data file.

This is a small snippet of code which makes it relatively easy to see how to use the raw data from Open Street Maps. For a complete rendering examples see the Open Street Maps wiki and the pyrender source code.
Key Concepts:
An OSM file is generated by selecting an area of interest at www.OpenStreetMap.org and selecting the export tab. Under the export tab, there is an option to export the map to 'OpenStreetMap XML Data'. If this is selected, then an XML file which contains all of the data for the selected region is generated. This XML file includes road, railways, trails, and land features among other things. The XML file has a a few header elements which define the XML standard, the data source, and the bounds on the data set. After that, the data file consists of a long list of nodes in the map. Each node describes one point on the surface of the earth. After the nodes, the ways are defined. A way consists of a list of nodes and tags. The nodes are are order and describe something like a road or a lake. The tag provide sufficient data to understand what the way represents. After the ways, come relations. Relations combine other elements and provide tags which area associated with those elements.
To render roads, only nodes and ways need to be considered.
When plotting lots of elements, Matplotlib can be sped up significantly (3X or more) by turning off autoscaling.
Since the ways are not ordered in the OSM file, z-ordering in matplotlib provides a nice way to control what has the most prominence.
So that the roads which are wider than 1 pixel have smooth transitions, the solid_capstyle and the solid_endstyle are set to ‘round’.
To simplify conversion of the XML data in the OSM file into an object which behaves like a dictionary, a script from ActiveState was used.
The Code:
#############################################################
## from http://code.activestate.com/recipes/534109-xml-to-python-data-structure/
import re
import xml.sax.handler
def xml2obj(src):
"""
A simple function to converts XML data into native Python object.
"""
non_id_char = re.compile('[^_0-9a-zA-Z]')
def _name_mangle(name):
return non_id_char.sub('_', name)
class DataNode(object):
def __init__(self):
self._attrs = {} # XML attributes and child elements
self.data = None # child text data
def __len__(self):
# treat single element as a list of 1
return 1
def __getitem__(self, key):
if isinstance(key, basestring):
return self._attrs.get(key,None)
else:
return [self][key]
def __contains__(self, name):
return self._attrs.has_key(name)
def __nonzero__(self):
return bool(self._attrs or self.data)
def __getattr__(self, name):
if name.startswith('__'):
# need to do this for Python special methods???
raise AttributeError(name)
return self._attrs.get(name,None)
def _add_xml_attr(self, name, value):
if name in self._attrs:
# multiple attribute of the same name are represented by a list
children = self._attrs[name]
if not isinstance(children, list):
children = [children]
self._attrs[name] = children
children.append(value)
else:
self._attrs[name] = value
def __str__(self):
return self.data or ''
def __repr__(self):
items = sorted(self._attrs.items())
if self.data:
items.append(('data', self.data))
return u'{%s}' % ', '.join([u'%s:%s' % (k,repr(v)) for k,v in items])
class TreeBuilder(xml.sax.handler.ContentHandler):
def __init__(self):
self.stack = []
self.root = DataNode()
self.current = self.root
self.text_parts = []
def startElement(self, name, attrs):
self.stack.append((self.current, self.text_parts))
self.current = DataNode()
self.text_parts = []
# xml attributes --> python attributes
for k, v in attrs.items():
self.current._add_xml_attr(_name_mangle(k), v)
def endElement(self, name):
text = ''.join(self.text_parts).strip()
if text:
self.current.data = text
if self.current._attrs:
obj = self.current
else:
# a text only node is simply represented by the string
obj = text or ''
self.current, self.text_parts = self.stack.pop()
self.current._add_xml_attr(_name_mangle(name), obj)
def characters(self, content):
self.text_parts.append(content)
builder = TreeBuilder()
if isinstance(src,basestring):
xml.sax.parseString(src, builder)
else:
xml.sax.parse(src, builder)
return builder.root._attrs.values()[0]
#############################################################
def render(myMap):
# make dictionary of node IDs
nodes = {}
for node in myMap['node']:
nodes[node['id']] = node
ways = {}
for way in myMap['way']:
ways[way['id']]=way
import pylab as p
renderingRules = {
'primary': dict(
linestyle = '-',
linewidth = 6,
color ='#ee82ee',
zorder = -1,
),
'primary_link': dict(
linestyle = '-',
linewidth = 6,
color = '#da70d6',
zorder = -1,
),
'secondary': dict(
linestyle = '-',
linewidth = 6,
color = '#d8bfd8',
zorder = -2,
),
'secondary_link': dict(
linestyle = '-',
linewidth = 6,
color = '#d8bfd8',
zorder = -2,
),
'tertiary': dict(
linestyle = '-',
linewidth = 4,
color = (0.0,0.0,0.7),
zorder = -3,
),
'tertiary_link': dict(
linestyle = '-',
linewidth = 4,
color = (0.0,0.0,0.7),
zorder = -3,
),
'residential': dict(
linestyle = '-',
linewidth = 1,
color = (0.1,0.1,0.1),
zorder = -99,
),
'unclassified': dict(
linestyle = ':',
linewidth = 1,
color = (0.5,0.5,0.5),
zorder = -1,
),
'default': dict(
linestyle = '-',
linewidth = 3,
color = 'b',
zorder = -1,
),
}
# get bounds from OSM data
minX = float(myMap['bounds']['minlon'])
maxX = float(myMap['bounds']['maxlon'])
minY = float(myMap['bounds']['minlat'])
maxY = float(myMap['bounds']['maxlat'])
fig = p.figure()
# by setting limits before hand, plotting is about 3 times faster
ax = fig.add_subplot(111,autoscale_on=False,xlim=(minX,maxX),ylim=(minY,maxY))
for idx,nodeID in enumerate(ways.keys()):
wayTags = ways[nodeID]['tag']
if not wayTags==None:
hwyTypeList = [d['v'] for d in wayTags if d['k']=='highway']
if len(hwyTypeList)>0:
wayType = hwyTypeList[0]
else:
wayType = None
else:
wayType = None
try:
if wayType in ['primary','primary_link',
'unclassified',
'secondary','secondary_link',
'tertiary','tertiary_link',
'residential',
'trunk','trunk_link',
'motorway','motorway_link',
]:
oldX = None
oldY = None
if wayType in renderingRules.keys():
thisRendering = renderingRules[wayType]
else:
thisRendering = renderingRules['default']
for nCnt,nID in enumerate(ways[nodeID]['nd']):
y = float(nodes[nID['ref']]['lat'])
x = float(nodes[nID['ref']]['lon'])
if oldX == None:
pass
else:
p.plot([oldX,x],[oldY,y],
marker = '',
linestyle = thisRendering['linestyle'],
linewidth = thisRendering['linewidth'],
color = thisRendering['color'],
solid_capstyle = 'round',
solid_joinstyle = 'round',
zorder = thisRendering['zorder'],
)
oldX = x
oldY = y
except KeyError:
pass
print'Done Plotting'
p.show()
########################################
src = file('map.osm')
myMap = xml2obj(src)
render(myMap)Testing Configuration:
- Windows 7
- PythonXY 2.5.6.1
- OpenStreetMap example data , mirrored example data, Map data © OpenStreetMap contributors, CC-BY-SA
Other Useful Links and references:
Questions Answered:
- How to visualize an Open Street Map from data
- How to plot a map
- How to draw an Open Street Map from the OSM file