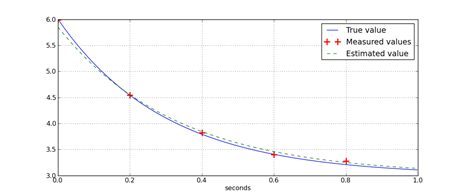
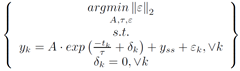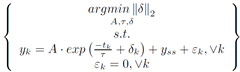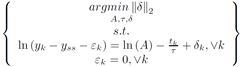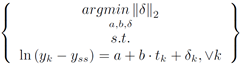If Panda3D 1.7.0 is added to Python using a ‘pth’ file, then JModelica 1.1b1 will load the wrong ‘mscvrt.dll’ and fail to initialize. This problem occurs:
In [1]: import jmodelica.examples.cstr as cstr
C:\Python26\lib\site-packages\jpype\_pykeywords.py:18: DeprecationWarning: the s
ets module is deprecated
import sets
---------------------------------------------------------------------------
OSError Traceback (most recent call last)C:\JModelica.org-1.1b1\work\<ipython console> in <module>()
C:\JModelica.org-1.1b1\Python\jmodelica\examples\cstr.py in <module>()
9 from jmodelica.initialization.ipopt import NLPInitialization
10 from jmodelica.initialization.ipopt import InitializationOptimizer
---> 11 from jmodelica.simulation.sundials import TrajectoryLinearInterpolation
12 from jmodelica.simulation.sundials import SundialsDAESimulator
13 from jmodelica.optimization import ipoptC:\JModelica.org-1.1b1\Python\jmodelica\simulation\sundials.py in <module>()
14
15 try:
---> 16 from pysundials import cvodes
17 from pysundials import ida
18 from pysundials import nvecserialC:\Python26\lib\site-packages\pysundials\cvodes.py in <module>()
38
39 import ctypes
---> 40 import sundials_core
41 import nvecserial
42C:\Python26\lib\site-packages\pysundials\sundials_core.py in <module>()
87 f.close()
88
---> 89 libc = loadlib("c")
90 try:
91 libc.fdopen.argtypes = [ctypes.c_int, ctypes.c_int]C:\Python26\lib\site-packages\pysundials\sundials_core.py in loadlib(libname)
63 lib = ctypes.CDLL(libpaths[libname])
64 except OSError, e:
---> 65 raise OSError("%s\nCannot load shared library %s. Please
check you config file and ensure the paths to the shared libraries are correct.
"%(e, libpaths[libname]))
66 return lib
67OSError: [Error 1114] A dynamic link library (DLL) initialization routine failed
Cannot load shared library C:\Panda3D-1.7.0\bin\msvcrt.dll. Please check you con
fig file and ensure the paths to the shared libraries are correct.
The occurs in pysundials because the util.find_library('msvcrt') in the ctypes module is attempting to load the ‘msvcrt.dll’ which is installed with Panda3D. This problem can be fixed by forcing pysundials to load a compatible msvcrt.dll file, rather than the most recent. This is done by modifying pysundials_core.py to point to the correct dll. The following change starting at line 42 will force a specific dll to be loaded. The path and dll to use will be specific to each system.
if os.name == "nt":
#clib = util.find_library('msvcrt')
clib = 'C:\\Program Files (x86)\\Java\\jdk1.6.0_17\\jre\\bin\\msvcrt.dll'
else:
clib = util.find_library('c')