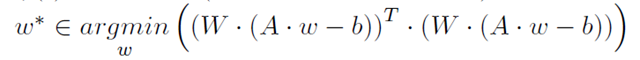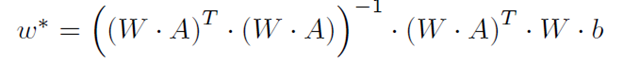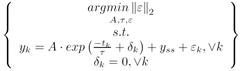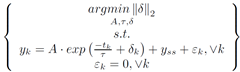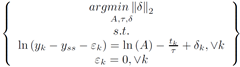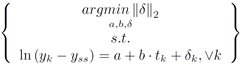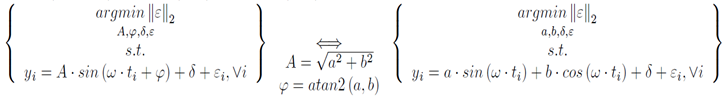One nice property of the Astar algorithm is that if a finite path exists between two nodes on an infinite order graph, and a good heuristic is chosen, then the Astar algorithm can find the shortest path with finite resources. One of the challenges is representing an infinite order graph in finite resources. Another challenge is making sure the heuristic is reasonable. However once those two issues are adequately addressed, searching for a shortest path on an infinite order graph can be done.
Wednesday, October 20, 2010
Sunday, October 10, 2010
Finding the shortest path between two points: An example of the A* algorithm in Python
Introduction:
One common challenge is finding the shortest or least expensive path between two points. This simple problem can represent many different engineering and information processing problems. One of the most familiar versions of this problem is finding the shortest or fastest way to travel through between two points on a map.A famous variant of this problem is the traveling salesman problem. To set up this kind of problem, a directed graph needs to be created. A directed graph defines the connection between nodes. It also defines the cost to travel between nodes.
Given an origin and a destination in the graph, there are many ways to find the shortest path (or least cost) path between the origin and destination. One way which is usually intractable is to do a brute force search. However, of the tractable ways to solve the problem, the A* algorithm can be fast and efficient if a few conditions are met: an approximate estimate of the cost to reach the destination from every point in the graph is available and this approximation is always equal to or less than the optimal cost to reach the destination.
An Example Problem:
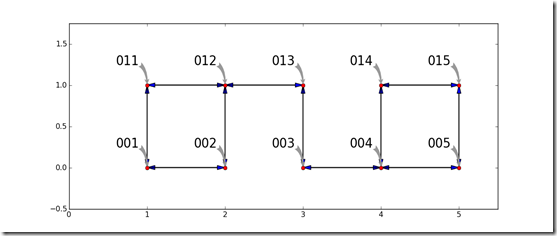
A shortest path problem has the goal of finding a path through a graph which costs the least. Consider the simple graph shown below. Each node is represented by a red circle. The ways to travel between the nodes (the edges, arcs, arrows, etc) are shown by arrows between the nodes. each node has a name which is called out. To make the graph interesting, there is no way to travel in one step between the pair of nodes in 002 and 003 and the other pair of 013 and 014. To keep the problem simple, the cost to travel on every edge is equal to the Euclidean distance along the edge.
The Astar algorithm can find a route from an origin to a destination node. For this example, the goal is to find a minimum cost route from node 001 to node 015. The graph is stored as a dictionary which has an entry for each node. This entry has a dictionary which defined the x and y coordinates of the node along with a list of nodes which can be reached. Furthermore, the approximate cost from each node to the destination is defined as the Euclidean distance from a given node to the destination. This distance satisfies the requirements for a good approximation in this model because it will always be equal or less than the best distance that can be achieved following the edges.
This implementation of the Astar algorithm is almost identical to the algorithm outlined in Wikipedia.
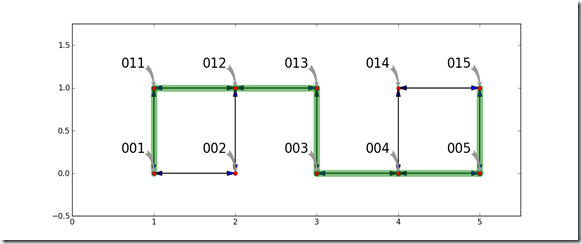
Once the Astar algorithm solves for the shortest path, the shortest path is visualized by laying it on top of the graph.
One key result can easily be seen in this example. By looking carefully at the graph, it should be obvious that there are other routes which can travel between the origin and destination with the same distance or cost. For some problems, there is not a single shortest path, there are potentially many paths which have the same cost. This algorithm will generate only one. There may be other routes which are the shortest path.
Code Example:
def Astar(start,goal,dist_between,neighbor_nodes,heuristic_estimate_of_dist):
closedset = set([]) # The set of nodes already evaluated.
openset = set([start]) # The set of tentative nodes to be evaluated.
# starts off containing initial node
came_from = set([]) # The map of navigated nodes.
g_score={start:0} # Distance from start along optimal path.
h_score={start:heuristic_estimate_of_dist(start,goal)}
f_score={start:h_score[start]} #Estimated total distance from start to goal through y.
came_from={start:None}
while len(openset)>0: # open set is not empty
#x := the node in openset having the lowest f_score[] value
bestX = None
for x in openset:
if bestX==None:
bestX = x
elif f_score[x] < f_score[bestX]:
bestX = x
x = bestX
if x == goal:
return reconstruct_path(came_from,came_from[goal])
openset.discard(x)
closedset.add(x)
neighbor_list = neighbor_nodes(x)
for y in neighbor_nodes(x):
if y in closedset:
continue
tentative_g_score = g_score[x] + dist_between(x,y)
if y not in openset:
openset.add(y)
tentative_is_better = True
elif tentative_g_score < g_score[y]:
tentative_is_better = True
else:
tentative_is_better = False
if tentative_is_better == True:
came_from[y] = x
g_score[y] = tentative_g_score
h_score[y] = heuristic_estimate_of_dist(y, goal)
f_score[y] = g_score[y] + h_score[y]
return None
def reconstruct_path(came_from, current_node):
if not came_from[current_node] == None:
p = reconstruct_path(came_from, came_from[current_node])
return (p + [current_node])
else:
return [current_node]
#####################################
if __name__=='__main__':
import pylab as p
graph = {
'001':dict(x=1, y=0,nextList=['002','011']),
# '002':dict(x=2, y=0,nextList=['001','003','012']),
# '003':dict(x=3, y=0,nextList=['002','004','013']),
'002':dict(x=2, y=0,nextList=['001','012']),
'003':dict(x=3, y=0,nextList=['004','013']),
'004':dict(x=4, y=0,nextList=['003','005','014']),
'005':dict(x=5, y=0,nextList=['004','015']),
'011':dict(x=1, y=1,nextList=['012','001']),
'012':dict(x=2, y=1,nextList=['011','013','002']),
# '013':dict(x=3, y=1,nextList=['012','014','003']),
# '014':dict(x=4, y=1,nextList=['013','015','004']),
'013':dict(x=3, y=1,nextList=['012','003']),
'014':dict(x=4, y=1,nextList=['015','004']),
'015':dict(x=5, y=1,nextList=['014','005']),
}
def neighbor_nodes(x):
return graph[x]['nextList']
def distance_between(x,y):
_x1 = graph[x]['x']
_x2 = graph[y]['x']
_y1 = graph[x]['y']
_y2 = graph[y]['y']
return ((_x1-_x2)**2+(_y1-_y2)**2)**(0.5)
def drawArrow(xFrom,xTo,yFrom,yTo):
length = ((xFrom-xTo)**2+(yFrom-yTo)**2)**(0.5)
head_len = 0.1
head_width = 0.05
dx = ((length-head_len)/length)*(xTo-xFrom)
dy = ((length-head_len)/length)*(yTo-yFrom)
p.arrow(xFrom,yFrom,dx,dy,
head_width=head_width,head_length=head_len)
def plotGraph(graph,ax):
first = True
for origin in graph.keys():
for dest in graph[origin]['nextList']:
xFrom = graph[origin]['x']
xTo = graph[dest]['x']
yFrom = graph[origin]['y']
yTo = graph[dest]['y']
drawArrow(xFrom,xTo,yFrom,yTo)
if first:
minX = xFrom
maxX = xFrom
minY = yFrom
maxY = yFrom
first = False
else:
minX = min(minX,xFrom)
maxX = max(maxX,xFrom)
minY = min(minY,yFrom)
maxY = max(maxY,yFrom)
p.plot([xFrom],[yFrom],'or')
ax.annotate(origin, xy=(xFrom,yFrom), xycoords='data',
xytext=(-50, 30), textcoords='offset points',
size=20,
#bbox=dict(boxstyle="round", fc="0.8"),
arrowprops=dict(arrowstyle="fancy",
fc="0.6", ec="none",
# patchB=el,
connectionstyle="angle3,angleA=0,angleB=-90"),
)
#p.axis([minX-0.25,maxX+0.25,minY-0.25,maxY+0.25])
def plotRoute(route,graph):
for idx,point in enumerate(route):
if idx < len(route)-1:
nextPoint = route[idx+1]
xFrom = graph[point]['x']
xTo = graph[nextPoint]['x']
yFrom = graph[point]['y']
yTo = graph[nextPoint]['y']
p.plot([xFrom,xTo],[yFrom,yTo],'-g',lw=10,alpha=0.5,solid_capstyle='round')
fig = p.figure()
ax = fig.add_subplot(111, autoscale_on=False, xlim=(0,5.5), ylim=(-0.5,1.75))
route = Astar('001','015',distance_between,neighbor_nodes,distance_between)
route.append('015')
print route
plotRoute(route,graph)
plotGraph(graph,ax)
print 'Done'
p.show()
References:
Tuesday, October 5, 2010
Beta release: How to render OpenStreetMaps using Python and Matplotlib
Introduction:
Open Street Maps is an collaboratively developed and open source map database. The entire OSM database or specific portions can be downloaded. The database includes information on roads, political boundaries, natural features, rail lines, trails, and much more. The website can generate output files with sufficient information to create custom and detailed surface street maps for many areas of the world. With Python and Matplotlib the XML data in an OpenStreetMaps OSM file can be rendered as a custom map can be rendered to meet specific needs. Below is an example of a map which can be generated from and OSM data file.

This is a small snippet of code which makes it relatively easy to see how to use the raw data from Open Street Maps. For a complete rendering examples see the Open Street Maps wiki and the pyrender source code.
Key Concepts:
An OSM file is generated by selecting an area of interest at www.OpenStreetMap.org and selecting the export tab. Under the export tab, there is an option to export the map to 'OpenStreetMap XML Data'. If this is selected, then an XML file which contains all of the data for the selected region is generated. This XML file includes road, railways, trails, and land features among other things. The XML file has a a few header elements which define the XML standard, the data source, and the bounds on the data set. After that, the data file consists of a long list of nodes in the map. Each node describes one point on the surface of the earth. After the nodes, the ways are defined. A way consists of a list of nodes and tags. The nodes are are order and describe something like a road or a lake. The tag provide sufficient data to understand what the way represents. After the ways, come relations. Relations combine other elements and provide tags which area associated with those elements.
To render roads, only nodes and ways need to be considered.
When plotting lots of elements, Matplotlib can be sped up significantly (3X or more) by turning off autoscaling.
Since the ways are not ordered in the OSM file, z-ordering in matplotlib provides a nice way to control what has the most prominence.
So that the roads which are wider than 1 pixel have smooth transitions, the solid_capstyle and the solid_endstyle are set to ‘round’.
To simplify conversion of the XML data in the OSM file into an object which behaves like a dictionary, a script from ActiveState was used.
The Code:
#############################################################
## from http://code.activestate.com/recipes/534109-xml-to-python-data-structure/
import re
import xml.sax.handler
def xml2obj(src):
"""
A simple function to converts XML data into native Python object.
"""
non_id_char = re.compile('[^_0-9a-zA-Z]')
def _name_mangle(name):
return non_id_char.sub('_', name)
class DataNode(object):
def __init__(self):
self._attrs = {} # XML attributes and child elements
self.data = None # child text data
def __len__(self):
# treat single element as a list of 1
return 1
def __getitem__(self, key):
if isinstance(key, basestring):
return self._attrs.get(key,None)
else:
return [self][key]
def __contains__(self, name):
return self._attrs.has_key(name)
def __nonzero__(self):
return bool(self._attrs or self.data)
def __getattr__(self, name):
if name.startswith('__'):
# need to do this for Python special methods???
raise AttributeError(name)
return self._attrs.get(name,None)
def _add_xml_attr(self, name, value):
if name in self._attrs:
# multiple attribute of the same name are represented by a list
children = self._attrs[name]
if not isinstance(children, list):
children = [children]
self._attrs[name] = children
children.append(value)
else:
self._attrs[name] = value
def __str__(self):
return self.data or ''
def __repr__(self):
items = sorted(self._attrs.items())
if self.data:
items.append(('data', self.data))
return u'{%s}' % ', '.join([u'%s:%s' % (k,repr(v)) for k,v in items])
class TreeBuilder(xml.sax.handler.ContentHandler):
def __init__(self):
self.stack = []
self.root = DataNode()
self.current = self.root
self.text_parts = []
def startElement(self, name, attrs):
self.stack.append((self.current, self.text_parts))
self.current = DataNode()
self.text_parts = []
# xml attributes --> python attributes
for k, v in attrs.items():
self.current._add_xml_attr(_name_mangle(k), v)
def endElement(self, name):
text = ''.join(self.text_parts).strip()
if text:
self.current.data = text
if self.current._attrs:
obj = self.current
else:
# a text only node is simply represented by the string
obj = text or ''
self.current, self.text_parts = self.stack.pop()
self.current._add_xml_attr(_name_mangle(name), obj)
def characters(self, content):
self.text_parts.append(content)
builder = TreeBuilder()
if isinstance(src,basestring):
xml.sax.parseString(src, builder)
else:
xml.sax.parse(src, builder)
return builder.root._attrs.values()[0]
#############################################################
def render(myMap):
# make dictionary of node IDs
nodes = {}
for node in myMap['node']:
nodes[node['id']] = node
ways = {}
for way in myMap['way']:
ways[way['id']]=way
import pylab as p
renderingRules = {
'primary': dict(
linestyle = '-',
linewidth = 6,
color ='#ee82ee',
zorder = -1,
),
'primary_link': dict(
linestyle = '-',
linewidth = 6,
color = '#da70d6',
zorder = -1,
),
'secondary': dict(
linestyle = '-',
linewidth = 6,
color = '#d8bfd8',
zorder = -2,
),
'secondary_link': dict(
linestyle = '-',
linewidth = 6,
color = '#d8bfd8',
zorder = -2,
),
'tertiary': dict(
linestyle = '-',
linewidth = 4,
color = (0.0,0.0,0.7),
zorder = -3,
),
'tertiary_link': dict(
linestyle = '-',
linewidth = 4,
color = (0.0,0.0,0.7),
zorder = -3,
),
'residential': dict(
linestyle = '-',
linewidth = 1,
color = (0.1,0.1,0.1),
zorder = -99,
),
'unclassified': dict(
linestyle = ':',
linewidth = 1,
color = (0.5,0.5,0.5),
zorder = -1,
),
'default': dict(
linestyle = '-',
linewidth = 3,
color = 'b',
zorder = -1,
),
}
# get bounds from OSM data
minX = float(myMap['bounds']['minlon'])
maxX = float(myMap['bounds']['maxlon'])
minY = float(myMap['bounds']['minlat'])
maxY = float(myMap['bounds']['maxlat'])
fig = p.figure()
# by setting limits before hand, plotting is about 3 times faster
ax = fig.add_subplot(111,autoscale_on=False,xlim=(minX,maxX),ylim=(minY,maxY))
for idx,nodeID in enumerate(ways.keys()):
wayTags = ways[nodeID]['tag']
if not wayTags==None:
hwyTypeList = [d['v'] for d in wayTags if d['k']=='highway']
if len(hwyTypeList)>0:
wayType = hwyTypeList[0]
else:
wayType = None
else:
wayType = None
try:
if wayType in ['primary','primary_link',
'unclassified',
'secondary','secondary_link',
'tertiary','tertiary_link',
'residential',
'trunk','trunk_link',
'motorway','motorway_link',
]:
oldX = None
oldY = None
if wayType in renderingRules.keys():
thisRendering = renderingRules[wayType]
else:
thisRendering = renderingRules['default']
for nCnt,nID in enumerate(ways[nodeID]['nd']):
y = float(nodes[nID['ref']]['lat'])
x = float(nodes[nID['ref']]['lon'])
if oldX == None:
pass
else:
p.plot([oldX,x],[oldY,y],
marker = '',
linestyle = thisRendering['linestyle'],
linewidth = thisRendering['linewidth'],
color = thisRendering['color'],
solid_capstyle = 'round',
solid_joinstyle = 'round',
zorder = thisRendering['zorder'],
)
oldX = x
oldY = y
except KeyError:
pass
print'Done Plotting'
p.show()
########################################
src = file('map.osm')
myMap = xml2obj(src)
render(myMap)Testing Configuration:
- Windows 7
- PythonXY 2.5.6.1
- OpenStreetMap example data , mirrored example data, Map data © OpenStreetMap contributors, CC-BY-SA
Other Useful Links and references:
Questions Answered:
- How to visualize an Open Street Map from data
- How to plot a map
- How to draw an Open Street Map from the OSM file
Saturday, July 31, 2010
How to start Open Office (with UNO services) from an external copy of Python
Problem Statement:
Demonstrate how to start Open Office from an external installation of Python so the pyuno library can be used to talk to the UNO interfaces in Open Office.
Target Application:
The purpose of this code snippet is to test a feature which automates Open Office from an external copy of Python (not the one shipped with Open Office).
Discussion:
There are several ways to start a process external to Python. One of the easiest is to use the os module’s system function. This allows a command to be passed to a shell, just like it was typed at the command line. This function starts a shell and passes a string to that shell, then return execution to python once the new shell terminates.
To start Open Office so that pyuno can automate it, some command line arguments must be passed. The following snippet illustrates how to use os.system(…) to start Open Office so pyuno can talk to it. While os.system is an easy way to start a process, it blocks execution until Open Office is closed.
import os workingDir = 'C:\\Program Files (x86)\\OpenOffice.org 3\\program' cmd = "\"\"" + workingDir + '\\soffice\" '+'"-accept=socket,host=localhost,port=8100;urp;StarOffice.NamingService"' # blocking call os.system(cmd) # this call block execution until open office terminated # do something after Open Office closes
To allow a Python script to continue to execute while Open Office is running, the subprocess module offers more powerful ways to launch and control the Open Office process. The following code snippet illustrates how to start Open Office as a listener for UNO calls using subprocess.Popen(…) .
import subprocess workingDir = 'C:\\Program Files (x86)\\OpenOffice.org 3\\program' cmd = workingDir + '\\soffice.exe' opts = '"-accept=socket,host=localhost,port=8100;urp;StarOffice.NamingService"' OOprocess = subprocess.Popen([cmd,opts]) # this call allows continued execution # do more stuff while Open Office runs
An important difference between using subprocess.Popen(…) and os.system(…) is that subprocess.Popen(…) eliminates the need to add double quotes around path names with spaces in Windows. In fact, if you add the double quotes you will get “WindowsError: [Error 5] Access is denied” because the path and file name are not properly interpreted.
Test Environment:
- PythonXY 2.6.5.1
- Open Office 3.2.0
- Windows 7
References:
Monday, July 26, 2010
How to prevent integer division errors in Python 2.x
When doing scientific computing, the usual assumption is that all numbers are floating point numbers. In Python 2.x, if two numbers are typed as integers, the result of division is the floor of the result. For example, dividing integer 3 by 4 results in 0 rather than 0.75. It is very easy to let subtle coding errors creep into a program because of this behavior.
>>> 3/4
0
>>> 3./4
0.75
What can make a bug really subtle is if a routine is defined which uses division. Then later a call is made with integers rather than floats.
>>> def testFunction(x,y):
... return x/y
...
>>> testFunction(3,4)
0
>>> testFunction(3.,4)
0.75
One way to avoid this issue is to guard all divisions in your code with a float conversion. However, this required a lot of diligence to maintain. A potentially easier solution is to import the division definitions from the __future__ module. Once this module is imported, it redefined how the ‘/’ operator behaves and eliminates this potential source of errors.
>>> from __future__ import division
>>> 3/4
0.75
Wednesday, July 21, 2010
Regression and Curve Fitting in Python – Pt 2
Weighted Curve Fitting.
Introduction
When using least-squares linear regression, an assumption in typical implementations is that the noise is Gaussian, white, and has the same statistics for all measurements. All of the solutions discussed in part 1 of this tutorial make this assumption including the polyfit function. This means that the regression will only work correctly is the measurement device always has the same statistics in its measurement errors. Sometimes, when data is collected, the noise statistics vary with each measurement. For example, this can happen when the background noise changes over time. Weighted least squares is a way to find fit a curve or find parameters when this occurs.
An Example
Consider a simplified ballistic problem. Ignoring the effect of air resistance, the vertical position of a projective is governed by its initial position, initial velocity, and the force of gravity. Since air resistance is not considered, the measured altitude of projectile is a closed form function of time:
The noise term at the end of the equation is the error introduced by the measurement system. The noise, varies as a function of time and is represented by a normal distribution with time varying variance. For this problem, assume the noise gets worse with each subsequent sample. The mean of the error in each measurement is zero and has a standard deviation equal to 1 plus 4 times the number of seconds since the measurements started:
This might happen because the measurement hardware heats up with each sample, or the projectile moves away from the sensor. To visualize how this distribution of measurement errors looks, the measurements are taken many times. Each experiment is plotted over the previous experiments. The density of the measurements provides a visual feel for how the increase in error spreads out the measurements. This is illustrated here:
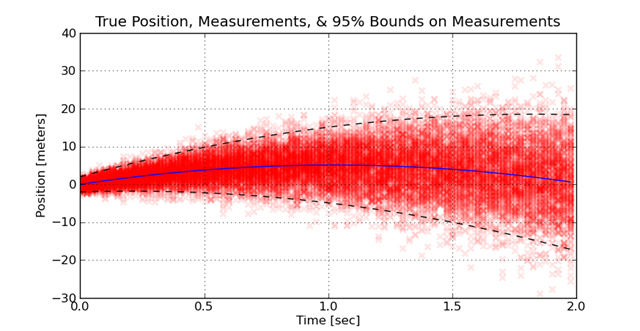 The challenge in this kind of problem is using the knowledge of the model of the behavior (e.g. the ballistics) and the model of the noise to find an optimal fit. If a suboptimal method is used, the error in the fit is significantly greater than if an optimal method is used. A single comparison on a one data set is insufficient to see the benefits of one approach versus another. When a large number of experiments are performed where the true value is know and the estimated values are know, the distribution of the estimation errors due to different approaches is visible. The following graph shows how using weighted least-squares versus least-squares assuming constant weights improves on the distribution of errors.
The challenge in this kind of problem is using the knowledge of the model of the behavior (e.g. the ballistics) and the model of the noise to find an optimal fit. If a suboptimal method is used, the error in the fit is significantly greater than if an optimal method is used. A single comparison on a one data set is insufficient to see the benefits of one approach versus another. When a large number of experiments are performed where the true value is know and the estimated values are know, the distribution of the estimation errors due to different approaches is visible. The following graph shows how using weighted least-squares versus least-squares assuming constant weights improves on the distribution of errors.
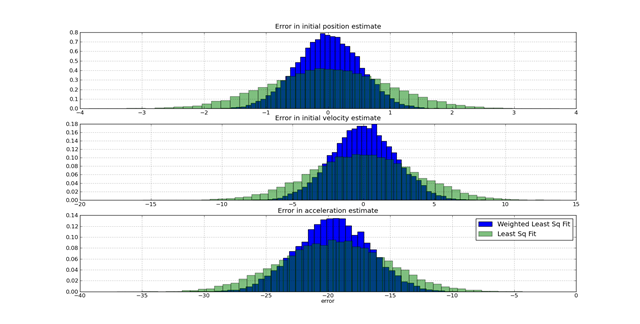 These graphs were generated from the following script:
These graphs were generated from the following script:
from random import normalvariate
from pylab import *
class System(object):
def __init__(self,p0=0.0,v0=10.0,a=-9.8):
self.p0 = p0
self.v0 = v0
self.a = a
def position(self,time):
return self.p0+self.v0*t+0.5*self.a*t**2
class Sensor(object):
def __init__(self,system=System(),errorStd=0.0):
self.system = system
self.errorStd = errorStd
def error(self,t=0):
try:
std = self.errorStd(t=t)
err = normalvariate(0,std)
except TypeError:
err = normalvariate(0,self.errorStd)
return err
class PositionSensor(Sensor):
def measure(self,t):
err = Sensor.error(self,t=t)
return self.system.position(t)+err
def errorStd(self,t):
try:
return self.errStd(t)
except TypeError:
return self.errStd
def weightedPolyFit(xList,yList,sigmaList,order=1,crossesAtZero=False):
'''fit the data using a weighted least squares for a polynomial model
xList is a list of input values
yList is a list of output values
sigmaList is a list with the standard deviation for each y value
order defines the order of the model,
order = 1 -> linear model
order = 2 -> quadratic model
crossesAtZero specifies whether the polynomial must be equal to zer
at x = 0
'''
fList = [(lambda x,n=n: x**n) for n in range(order,-1,-1)]
if crossesAtZero:
# eliminate the first column so the model corsses at 0
del fList[0]
# build row for each element in y
bList = []
A_List = []
for (thisX,thisY) in zip(xList,yList):
bList.append(thisY)
A_Row = [f(thisX) for f in fList]
A_List.append(A_Row)
W = diag([1.0 /sigma for sigma in sigmaList])
b = matrix(bList).T
A = matrix(A_List)
b2 = W*b
A2 = W*A
w = inv(A2.T*A2)*A2.T*b2
return w.T.tolist()[0]
if __name__=='__main__':
import random
errStdFun = lambda t: 1 + 4.0*t
random.seed(0)
p0True = 0.0
v0True = 10.0
aTrue = 9.8
s = System()
p = PositionSensor(s,errStdFun)
tSamples = arange(0,2,0.025)
pErr1List = []
pErr2List = []
vErr1List = []
vErr2List = []
aErr1List = []
aErr2List = []
for i in range(0,20000):
measuredPosition = [p.measure(t) for t in tSamples]
xList = tSamples
yListMeasured = measuredPosition
sigmaList = [p.errorStd(t) for t in tSamples]
w = weightedPolyFit(xList,yListMeasured,sigmaList,order=2)
p0Est = w[2]
v0Est = w[1]
aEst = w[0]*2
pErr1List.append(p0Est-p0True)
vErr1List.append(v0Est-v0True)
aErr1List.append(aEst-aTrue)
w2 = polyfit(xList,yListMeasured,2)
p0Est2 = w2[2]
v0Est2 = w2[1]
aEst2 = w2[0]*2
pErr2List.append(p0Est2-p0True)
vErr2List.append(v0Est2-v0True)
aErr2List.append(aEst2-aTrue)
figure(1)
subplot(3,1,1)
hist(pErr1List,50,normed=True)
hist(pErr2List,50,normed=True,alpha=0.5)
grid(True)
title('Error in initial position estimate')
subplot(3,1,2)
hist(vErr1List,50,normed=True)
hist(vErr2List,50,normed=True,alpha=0.5)
grid(True)
title('Error in initial velocity estimate')
subplot(3,1,3)
hist(aErr1List,50,normed=True,label='Weighted Least Sq Fit')
hist(aErr2List,50,normed=True,label='Least Sq Fit',alpha=0.5)
legend()
grid(True)
xlabel('error')
title('Error in acceleration estimate')
show() Some Theory: Finding the best fit
Recall from pt 1, that a least-squares fit is performed by reducing the equations to a matrix expression,
![]() then using the KKT conditions to find the weights which minimize the sum of errors squared.
then using the KKT conditions to find the weights which minimize the sum of errors squared.
In weighted least-squares, each error can have a different relative importance in the minimization problem. Usually, this weighting is equal to the inverse of the standard deviation of the error and each error is assumed to be uncorrelated. If these conditions are met, the relative weighting is in a diagonal matrix. Using the KKT conditions, this minimization problem,
is solved using
The solved example
To solve this problem, a system class and a sensor class is created. The sensor class is subclassed into a position sensor. The system class provides a model of the true behavior of the system. The sensor class provides a model of the data measured by a sensor which detecting the true position of the system in the presence of noise.
The weightedPolyFit function, in the listing, provides the logic to generate a weighted fit for parameters in a polynomial equation, which describes the position of the projectile.
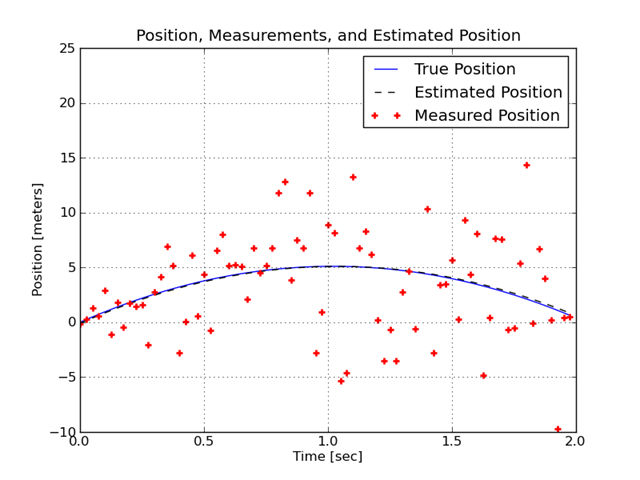
This plot shows the true trajectory of the projectile, the measured positions, and the estimated positions.
The full code for the example
from random import normalvariate
from pylab import *
class System(object):
def __init__(self,p0=0.0,v0=10.0,a=-9.8):
self.p0 = p0
self.v0 = v0
self.a = a
def position(self,time):
return self.p0+self.v0*t+0.5*self.a*t**2
class Sensor(object):
def __init__(self,system=System(),errorStd=0.0):
self.system = system
self.errorStd = errorStd
def error(self,t=0):
try:
std = self.errorStd(t=t)
err = normalvariate(0,std)
except TypeError:
err = normalvariate(0,self.errorStd)
return err
class PositionSensor(Sensor):
def measure(self,t):
err = Sensor.error(self,t=t)
return self.system.position(t)+err
def errorStd(self,t):
try:
return self.errStd(t)
except TypeError:
return self.errStd
def weightedPolyFit(xList,yList,sigmaList,order=1,crossesAtZero=False):
'''fit the data using a weighted least squares for a polynomial model
xList is a list of input values
yList is a list of output values
sigmaList is a list with the standard deviation for each y value
order defines the order of the model,
order = 1 -> linear model
order = 2 -> quadratic model
crossesAtZero specifies whether the polynomial must be equal to zer
at x = 0
'''
fList = [(lambda x,n=n: x**n) for n in range(order,-1,-1)]
if crossesAtZero:
# eliminate the first column so the model corsses at 0
del fList[0]
# build row for each element in y
bList = []
A_List = []
for (thisX,thisY) in zip(xList,yList):
bList.append(thisY)
A_Row = [f(thisX) for f in fList]
A_List.append(A_Row)
W = diag([1.0 /sigma for sigma in sigmaList])
b = matrix(bList).T
A = matrix(A_List)
b2 = W*b
A2 = W*A
w = inv(A2.T*A2)*A2.T*b2
return w.T.tolist()[0]
if __name__=='__main__':
import random
errStdFun = lambda t: 1 + 4.0*t
random.seed(0)
s = System()
p = PositionSensor(s,errStdFun)
tSamples = arange(0,2,0.025)
truePosition = [s.position(t) for t in tSamples]
measuredPosition = [p.measure(t) for t in tSamples]
xList = tSamples
yListMeasured = measuredPosition
sigmaList = [p.errorStd(t) for t in tSamples]
w = weightedPolyFit(xList,yListMeasured,sigmaList,order=2)
p0Est = w[2]
v0Est = w[1]
aEst = w[0]*2
print '..p0Est = %f, v0Est=%f, aEst = %f' % (p0Est,v0Est,aEst)
sEst = System(p0=p0Est,v0=v0Est,a=aEst)
est1Position = [sEst.position(t) for t in tSamples]
figure(1)
plot(tSamples,truePosition)
plot(tSamples,est1Position,'--k')
plot(tSamples,measuredPosition,'+r',markeredgewidth=2)
grid(True)
ylabel('Position [meters]')
xlabel('Time [sec]')
title('Position, Measurements, and Estimated Position')
legend(['True Position','Estimated Position','Measured Position'])
savefig('Position and Measurements.png')
figure(2)
err3Sigma = [2.0*p.errorStd(t) for t in tSamples]
errorbar(tSamples,truePosition,err3Sigma)
#plot(tSamples,truePosition)
plot(tSamples,est1Position,'--k')
plot(tSamples,measuredPosition,'+r',markeredgewidth=2)
grid(True)
ylabel('Position [meters]')
xlabel('Time [sec]')
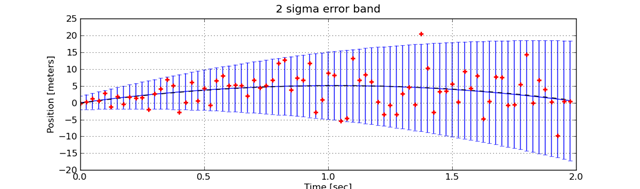
title('2 sigma error band')
savefig('ErrorBand.png')
figure(3)
for i in range(0,250):
measuredPosition = [p.measure(t) for t in tSamples]
plot(tSamples,measuredPosition,'xr',alpha=0.1,markeredgewidth=2)
plot(tSamples,truePosition,'-b')
upperLimit = [ 2.0*p.errorStd(t)+s.position(t) for t in tSamples]
lowerLimit = [-2.0*p.errorStd(t)+s.position(t) for t in tSamples]
plot(tSamples,upperLimit,'--k')
plot(tSamples,lowerLimit,'--k')
grid(True)
ylabel('Position [meters]')
xlabel('Time [sec]')
title('True Position, Measurements, & 95% Bounds on Measurements')
show()
See part 1 here.
All text is copyright © 2010, Ed Tate, All Rights Reserved.
All software and example codes are subject to the MIT License
Copyright (c) 2010, Ed Tate, Permission is hereby granted, free of charge, to any person obtaining a copy of this software and associated documentation files (the "Software"), to deal in the Software without restriction, including without limitation the rights to use, copy, modify, merge, publish, distribute, sublicense, and/or sell copies of the Software, and to permit persons to whom the Software is furnished to do so, subject to the following conditions: The above copyright notice and this permission notice shall be included in all copies or substantial portions of the Software.
THE SOFTWARE IS PROVIDED "AS IS", WITHOUT WARRANTY OF ANY KIND, EXPRESS OR IMPLIED, INCLUDING BUT NOT LIMITED TO THE WARRANTIES OF MERCHANTABILITY, FITNESS FOR A PARTICULAR PURPOSE AND NONINFRINGEMENT. IN NO EVENT SHALL THE AUTHORS OR COPYRIGHT HOLDERS BE LIABLE FOR ANY CLAIM, DAMAGES OR OTHER LIABILITY, WHETHER IN AN ACTION OF CONTRACT, TORT OR OTHERWISE, ARISING FROM, OUT OF OR IN CONNECTION WITH THE SOFTWARE OR THE USE OR OTHER DEALINGS IN THE SOFTWARE.
Saturday, July 17, 2010
A simple example of how to add engineering units to numbers in Python
When building numeric analyses, one source of errors is units. It is very common to merge data from multiple sources, where each source uses a different, and incompatible set of engineering units. Once an error like this is introduced, it can be difficult to find the error and correct it.
This tutorial shows how to create a class which behaves like a floating point number, but carries a descriptive string which can be used for various purposes in a program. This is a very simple approach is provided to understand how to create a class which inherits from an immutable class in python.
Use Case:
The use case of this class is simple. It is intended to allow a unit to be attached to a floating point value when the value is passed between functions. However, the units will not be preserved through math operations. There are several libraries which will do all of this.
>>x = FloatWithUnits(3.1415,'miles')
>>y = FloatWithUnits(2.7182,'km')
>>print x
... 3.1415+0.0j miles
>>print y
... 2.7182+0.0j km
>>z = x*y
>>print z
... 8.5392253
Solution and Discussion:
Any class which emulates numeric types needs to override many class methods. By inheriting from an existing type, like a float, all of these methods will be defined with default behavior. For this problem, the challenge is to attach and engineering unit, while preserving all of the methods of a floating point number. The obvious approach to this problem is to create a class which inherits from floats.
When inheriting from an immutable type, things are a little different than inheriting from other classes. The __new__ method must generally be overridden. Otherwise, the __new__ method will prevent an overridden __init__ method from executing. Also, since we’d like the class to display properly, the __str__ and __repr__ methods are overridden. Here is the new class:
class FloatWithUnits(float):
def __new__(cls,value,units=None):
return float.__new__(cls,value)
def __init__(self,value,units=None):
self.units=units
def __repr__(self):
return 'FloatWithUnits('+str(self.real)+'+'+str(self.imag)+'j,"'+self.units+'")'
def __str__(self):
return str(self.real)+'+'+str(self.imag)+'j '+self.units
if __name__=='__main__':
print FloatWithUnits(4.543)**2
import unittest
class Test_FloatWithUnits(unittest.TestCase):
def setUp(self):
pass
def test_DefaultInstanciation(self):
self.assertTrue(FloatWithUnits(1.45)==1.45)
self.assertAlmostEqual(FloatWithUnits(1.45)*2,2*1.45)
self.assertTrue(FloatWithUnits(-1.45)<0)
self.assertTrue(FloatWithUnits(1.45)>0)
def test_Units(self):
x = FloatWithUnits(2.3,'miles')
#print x.units
self.assertTrue(x.units=='miles')
#unittest.main()
suite = unittest.TestLoader().loadTestsFromTestCase(Test_FloatWithUnits)
unittest.TextTestRunner(verbosity=2).run(suite)
What doesn’t work and why.
As important as it is to see a working example, seeing a nonworking example is useful. A naive approach to solving this problem is to inherit from float and simply override the __init__ method. This will fail for several reasons, but, the most perplexing error will be the related to the number of arguments during class creation. Try the following code snippet.
class FloatWithUnits(float):
def __init__(self,value,units=None):
super(FloatWithUnits,self).__init__()
self.units=units
>>x = FloatWithUnits(2.3,'miles’)
... TypeError: float() takes at most 1 argument (2 given)
This exception occurs because the __new__ method for float only accepts one value. The inheritance of floats in this class brings in the float __new__ method, and the __init__ method never has a chance to run.
Related Libraries and Packages:
There are several libraries which add engineering units to scalar and matrix math. Here are a few of them:
- http://pypi.python.org/pypi/units/
- This library offers the ability to turn off the units math once code is working resulting in improved performance: http://russp.us/scalar-guide.htm
- http://pypi.python.org/pypi/magnitude/0.9.1
- This library works with both scalar and matrix math in scipy/numpy: http://pypi.python.org/pypi/piquant/0.1
References:
- http://www.python.org/download/releases/2.2/descrintro/
- http://code.activestate.com/recipes/303059-overriding-__new__-for-attribute-initialization/
- http://docs.python.org/release/2.5.2/ref/numeric-types.html
All software and example codes are subject to the MIT License
Copyright (c) 2010, Ed Tate, Permission is hereby granted, free of charge, to any person obtaining a copy of this software and associated documentation files (the "Software"), to deal in the Software without restriction, including without limitation the rights to use, copy, modify, merge, publish, distribute, sublicense, and/or sell copies of the Software, and to permit persons to whom the Software is furnished to do so, subject to the following conditions: The above copyright notice and this permission notice shall be included in all copies or substantial portions of the Software.
THE SOFTWARE IS PROVIDED "AS IS", WITHOUT WARRANTY OF ANY KIND, EXPRESS OR IMPLIED, INCLUDING BUT NOT LIMITED TO THE WARRANTIES OF MERCHANTABILITY, FITNESS FOR A PARTICULAR PURPOSE AND NONINFRINGEMENT. IN NO EVENT SHALL THE AUTHORS OR COPYRIGHT HOLDERS BE LIABLE FOR ANY CLAIM, DAMAGES OR OTHER LIABILITY, WHETHER IN AN ACTION OF CONTRACT, TORT OR OTHERWISE, ARISING FROM, OUT OF OR IN CONNECTION WITH THE SOFTWARE OR THE USE OR OTHER DEALINGS IN THE SOFTWARE.
Saturday, June 5, 2010
How to launch and terminate Matlab from Python
The recommended way to automate Matlab is to use COM API. However, there are situations where COM is not desired. In this case, the following Python script will launch Matlab, then find the process ID to provide the ability to terminate the process if needed. The reason for this is because occasionally when Matlab is launched from the command line, it shells a new process which is independent of the launching shell. Therefore, to monitor and terminate the Matlab process (say if a script goes awry), the Matlab process and its ID need to be found in the windows process list. Once the process ID is known, it can be treated as any other process by Python.
import wmi
c = wmi.WMI()
import os
os.popen('matlab')
print ‘Matlab launched’
raw_input('Press Enter to continue...')
print ‘Looking for Matlab in process list’
for process in c.Win32_Process(name='matlab.exe'):
print process.ProcessId, process.Name
found = True
if found:
raw_input('Press Enter to terminate Matlab...')
process.Terminate()
else:
print '!!! Matlab not found...'
This code was tested with Matlab 2007b and Python 2.5.1 with PyWin32 and wmi on windows XP.
Thursday, May 20, 2010
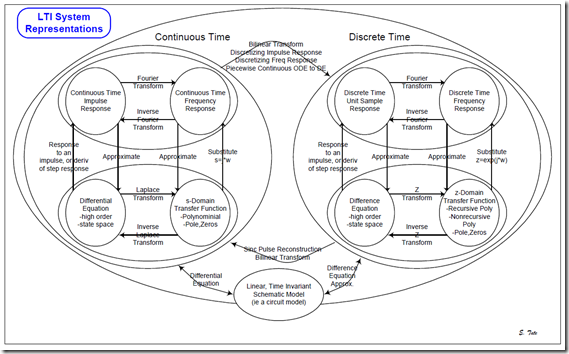
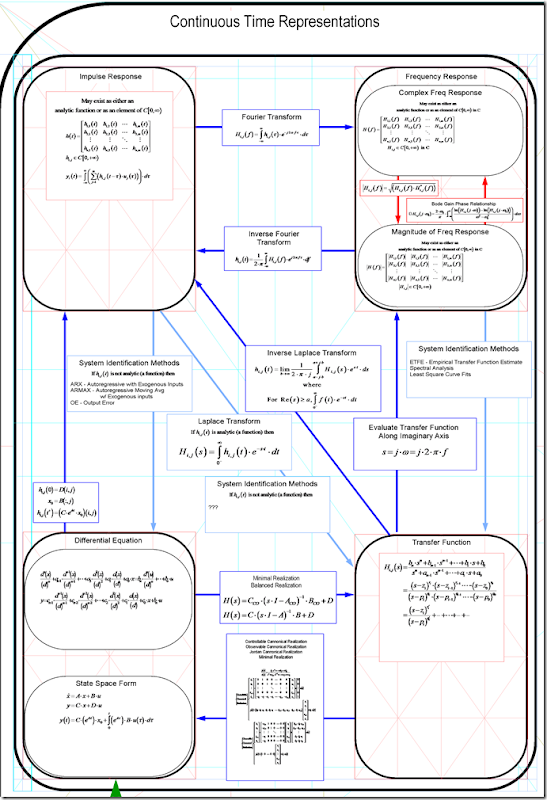
Linear Time Invariant System – Representations and conversions between.
Using this chart, you can see how to convert among linear system representations. It shows how to convert …
- a linear continuous-time system into a linear discrete-time system
- between an impulse response model and a frequency response model
- between a differential equation and an impulse response model
- between the s-domain and a frequency response model
- between the s-domain and differential equations
- between difference equations and differential equations
- and more!
Once you see how these representations are all interchangeable, it is easy to see how to reuse the different tools, which are usually specific to a given representation.
The continuous-time models and equations for conversion are shown below.
This entry answers the following questions (and more…):
- How to convert an s-domain model into a differential equation.
- How to convert a transfer function into a differential equation.
- How to convert an impulse response into a differential equation.
- How to convert an impulse response into a frequency response.
- How to convert an impulse response into a transfer function.
- …..
All text and images are release under the Creative Commons Attribution 3.0 License as long as this blog and the author (Ed Tate) are attributed.
Sunday, April 25, 2010
PythonXY 2.6.2 + Panda3d 1.7.0 + JModelica 1.1b1 – How to get to work together
If Panda3D 1.7.0 is added to Python using a ‘pth’ file, then JModelica 1.1b1 will load the wrong ‘mscvrt.dll’ and fail to initialize. This problem occurs:
In [1]: import jmodelica.examples.cstr as cstr
C:\Python26\lib\site-packages\jpype\_pykeywords.py:18: DeprecationWarning: the s
ets module is deprecated
import sets
---------------------------------------------------------------------------
OSError Traceback (most recent call last)C:\JModelica.org-1.1b1\work\<ipython console> in <module>()
C:\JModelica.org-1.1b1\Python\jmodelica\examples\cstr.py in <module>()
9 from jmodelica.initialization.ipopt import NLPInitialization
10 from jmodelica.initialization.ipopt import InitializationOptimizer
---> 11 from jmodelica.simulation.sundials import TrajectoryLinearInterpolation
12 from jmodelica.simulation.sundials import SundialsDAESimulator
13 from jmodelica.optimization import ipoptC:\JModelica.org-1.1b1\Python\jmodelica\simulation\sundials.py in <module>()
14
15 try:
---> 16 from pysundials import cvodes
17 from pysundials import ida
18 from pysundials import nvecserialC:\Python26\lib\site-packages\pysundials\cvodes.py in <module>()
38
39 import ctypes
---> 40 import sundials_core
41 import nvecserial
42C:\Python26\lib\site-packages\pysundials\sundials_core.py in <module>()
87 f.close()
88
---> 89 libc = loadlib("c")
90 try:
91 libc.fdopen.argtypes = [ctypes.c_int, ctypes.c_int]C:\Python26\lib\site-packages\pysundials\sundials_core.py in loadlib(libname)
63 lib = ctypes.CDLL(libpaths[libname])
64 except OSError, e:
---> 65 raise OSError("%s\nCannot load shared library %s. Please
check you config file and ensure the paths to the shared libraries are correct.
"%(e, libpaths[libname]))
66 return lib
67OSError: [Error 1114] A dynamic link library (DLL) initialization routine failed
Cannot load shared library C:\Panda3D-1.7.0\bin\msvcrt.dll. Please check you con
fig file and ensure the paths to the shared libraries are correct.
The occurs in pysundials because the util.find_library('msvcrt') in the ctypes module is attempting to load the ‘msvcrt.dll’ which is installed with Panda3D. This problem can be fixed by forcing pysundials to load a compatible msvcrt.dll file, rather than the most recent. This is done by modifying pysundials_core.py to point to the correct dll. The following change starting at line 42 will force a specific dll to be loaded. The path and dll to use will be specific to each system.
if os.name == "nt":
#clib = util.find_library('msvcrt')
clib = 'C:\\Program Files (x86)\\Java\\jdk1.6.0_17\\jre\\bin\\msvcrt.dll'
else:
clib = util.find_library('c')
An interesting tool - Pyspread
This is an interesting project: Pyspread. It is still a little rough, but shows a lot of promise as a way to use Python. Basically it is a spreadsheet built in Python and using Python to define cell behavior. I’ve installed it under PythonXY and it appears to work. A little slow, but not bad for a beta.
Alternatives to a prototyping tools that make python easier to use are:
- Reinteract - an interactive workbook
- Resolver One Spreadsheet (free for open source projects)
- IPython
- Pyshell
- SPE – an IDE
- Pyscripter – an IDE
- Orange - a visual data analysis environment
- Vision HPC – a visual parallel programming environment
In general some alternative environments to prototype behavior include:
- Bean Sheet for Java
- Scheme in a Grid (SIAG) for Scheme
Wednesday, April 21, 2010
How to get Panda3D to work with PythonXY
This note applies to Panda3d ver 1.7.0 and PythonXY ver 2.6.2 on a windows system.
- Install PythonXY.
- Install Panda3D, however do NOT set it as the default python interpreter.
- Add a ‘pth’ file to the python site-packages directory. I created a file named panda.pth and saved it at “C:\Python26\Lib\site-packages”. The file had the following contents:
C:/Panda3D-1.7.0
C:/Panda3D-1.7.0/bin
To check that the installation works, use an example from the Panda3D manual.
from direct.showbase.ShowBase import ShowBase class MyApp(ShowBase): def __init__(self): ShowBase.__init__(self) app = MyApp() app.run()
Wednesday, April 7, 2010
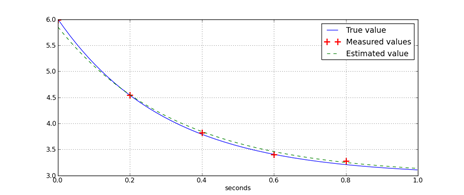
How to fit exponential decay – An example in Python
Linear least squares can be used to fit an exponent. However, the linear least square problem that is formed, has a structure and behavior that requires some careful consideration to fully understand. Usually, fitting is used because the data is noisy. If only the number of data points equal to the number of free variables in system of equations is used, the estimate of parameters will generally be poor.
For example, a common problem is estimating the parameters or coefficients for cooling. For example, a mass is heated to a steady temperature, then left to cool. Ignoring a lot of detail, a model of this behavior can be described by a simple first order, ordinary differential equation:
![]() In this equation, T is the temperature of the object, T0 is the ambient temperature, and h is a coefficient of hear transfer. When T0 is held constant and T(t=0) is not equal to T0, T(t) is described by an exponential decay function.
In this equation, T is the temperature of the object, T0 is the ambient temperature, and h is a coefficient of hear transfer. When T0 is held constant and T(t=0) is not equal to T0, T(t) is described by an exponential decay function.
An exponential decay function is
For a system whose behavior can be defined by exponential decay, the parameters for the decay function can be found using least-squares. Since the data usually has measurement errors, the measured data from an exponential decay will usually contain an error term.
![]() Ideally, this equation could be directly set up as a linear least squares problem. However, minimizing the norm of epsilon, requires solution via methods other than linear least squares. To formulate this problem as a linear least squares minimization, a new error term inside the exponent is introduced, del.
Ideally, this equation could be directly set up as a linear least squares problem. However, minimizing the norm of epsilon, requires solution via methods other than linear least squares. To formulate this problem as a linear least squares minimization, a new error term inside the exponent is introduced, del.
The usual way to set this problem up is to minimize the norm of epsilon.
However, if the problem is set up to minimize the 2-norm of del, then a linear least squared minimization can be formed.
To linearize this problem, the terms in the constraints are rearranged, the natural log of each side is taken, and the properties of logarithms are isolate terms.
The problem statement is simplified by eliminating the epsilon term.
Furthermore, this constrained optimization problem is restated as an unconstrained optimization problem.
Least squares can be used to solve this problem.
The reason for this development is to understand what is really solved by this formulation. When this technique is used to solve for an exponential delay function’s parameters, the measurement errors are not minimized. An artificial term which resembles an error in time is minimized.
The following python code shows how to solve this kind of problem.
from pylab import *
from math import log
def fitExponent(tList,yList,ySS=0):
'''
This function finds a
tList in sec
yList - measurements
ySS - the steady state value of y
returns
amplitude of exponent
tau - the time constant
'''
bList = [log(max(y-ySS,1e-6)) for y in yList]
b = matrix(bList).T
rows = [ [1,t] for t in tList]
A = matrix(rows)
#w = (pinv(A)*b)
(w,residuals,rank,sing_vals) = lstsq(A,b)
tau = -1.0/w[1,0]
amplitude = exp(w[0,0])
return (amplitude,tau)
if __name__=='__main__':
import random
tList = arange(0.0,1.0,0.001)
tSamples = arange(0.0,1.0,0.2)
random.seed(0.0)
tau = 0.3
amplitude = 3
ySS = 3
yList = amplitude*(exp(-tList/tau))+ySS
ySamples = amplitude*(exp(-tSamples/tau))+ySS
yMeasured = [y+random.normalvariate(0,0.05) for y in ySamples]
#print yList
(amplitudeEst,tauEst) = fitExponent(tSamples,yMeasured,ySS)
print ('Amplitude estimate = %f, tau estimate = %f'
% (amplitudeEst,tauEst))
yEst = amplitudeEst*(exp(-tList/tauEst))+ySS
figure(1)
plot(tList,yList,'b')
plot(tSamples,yMeasured,'+r',markersize=12,markeredgewidth=2)
plot(tList,yEst,'--g')
xlabel('seconds')
legend(['True value','Measured values','Estimated value'])
grid(True)
show()
All text is copyright © 2010, Ed Tate, All Rights Reserved.
All software and example codes are subject to the MIT License
Copyright (c) 2010, Ed Tate, Permission is hereby granted, free of charge, to any person obtaining a copy of this software and associated documentation files (the "Software"), to deal in the Software without restriction, including without limitation the rights to use, copy, modify, merge, publish, distribute, sublicense, and/or sell copies of the Software, and to permit persons to whom the Software is furnished to do so, subject to the following conditions: The above copyright notice and this permission notice shall be included in all copies or substantial portions of the Software.
THE SOFTWARE IS PROVIDED "AS IS", WITHOUT WARRANTY OF ANY KIND, EXPRESS OR IMPLIED, INCLUDING BUT NOT LIMITED TO THE WARRANTIES OF MERCHANTABILITY, FITNESS FOR A PARTICULAR PURPOSE AND NONINFRINGEMENT. IN NO EVENT SHALL THE AUTHORS OR COPYRIGHT HOLDERS BE LIABLE FOR ANY CLAIM, DAMAGES OR OTHER LIABILITY, WHETHER IN AN ACTION OF CONTRACT, TORT OR OTHERWISE, ARISING FROM, OUT OF OR IN CONNECTION WITH THE SOFTWARE OR THE USE OR OTHER DEALINGS IN THE SOFTWARE.
Tuesday, April 6, 2010
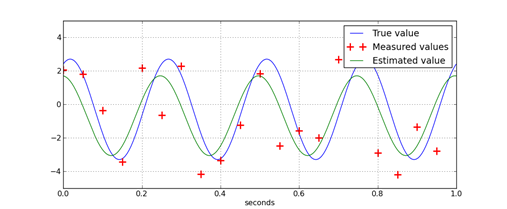
How to fit a sine wave – An example in Python
If the frequency of a signal is known, the amplitude, phase, and bias on the signal can be estimated using least-squares regression. The key concept that makes this possible is the fact that a sine wave of arbitrary phase can be represented by the sum of a sin wave and a cosine wave.
The regression problem to find the amplitude and phase is an optimization problem. However, it is not easily solved when using the amplitude and phase directly. This is because the problem is nonconvex; it has multiple minima. By applying trigonometric identities, an equivalent problem, which is convex, is formed.
Once the regression problem is in this form, the solution is found by forming linear least squares problem. The python function illustrates how to do this. Since python’s function work in radians but most people prefer Hertz and degrees, this script performs those conversions.
from pylab import *
from math import atan2
def fitSine(tList,yList,freq):
'''
freq in Hz
tList in sec
returns
phase in degrees
'''
b = matrix(yList).T
rows = [ [sin(freq*2*pi*t), cos(freq*2*pi*t), 1] for t in tList]
A = matrix(rows)
(w,residuals,rank,sing_vals) = lstsq(A,b)
phase = atan2(w[1,0],w[0,0])*180/pi
amplitude = norm([w[0,0],w[1,0]],2)
bias = w[2,0]
return (phase,amplitude,bias)
if __name__=='__main__':
import random
tList = arange(0.0,1.0,0.001)
tSamples = arange(0.0,1.0,0.05)
random.seed(0.0)
phase = 65
amplitude = 3
bias = -0.3
frequency = 4
yList = amplitude*sin(tList*frequency*2*pi+phase*pi/180.0)+bias
ySamples = amplitude*sin(tSamples*frequency*2*pi+phase*pi/180.0)+bias
yMeasured = [y+random.normalvariate(0,2) for y in ySamples]
#print yList
(phaseEst,amplitudeEst,biasEst) = fitSine(tSamples,yMeasured,frequency)
print ('Phase estimate = %f, Amplitude estimate = %f, Bias estimate = %f'
% (phaseEst,amplitudeEst,biasEst))
yEst = amplitudeEst*sin(tList*frequency*2*pi+phaseEst*pi/180.0)+biasEst
figure(1)
plot(tList,yList,'b')
plot(tSamples,yMeasured,'+r',markersize=12,markeredgewidth=2)
plot(tList,yEst,'-g')
xlabel('seconds')
legend(['True value','Measured values','Estimated value'])
grid(True)
show()
All text is copyright © 2010, Ed Tate, All Rights Reserved.
All software and example codes are subject to the MIT License
Copyright (c) 2010, Ed Tate, Permission is hereby granted, free of charge, to any person obtaining a copy of this software and associated documentation files (the "Software"), to deal in the Software without restriction, including without limitation the rights to use, copy, modify, merge, publish, distribute, sublicense, and/or sell copies of the Software, and to permit persons to whom the Software is furnished to do so, subject to the following conditions: The above copyright notice and this permission notice shall be included in all copies or substantial portions of the Software.
THE SOFTWARE IS PROVIDED "AS IS", WITHOUT WARRANTY OF ANY KIND, EXPRESS OR IMPLIED, INCLUDING BUT NOT LIMITED TO THE WARRANTIES OF MERCHANTABILITY, FITNESS FOR A PARTICULAR PURPOSE AND NONINFRINGEMENT. IN NO EVENT SHALL THE AUTHORS OR COPYRIGHT HOLDERS BE LIABLE FOR ANY CLAIM, DAMAGES OR OTHER LIABILITY, WHETHER IN AN ACTION OF CONTRACT, TORT OR OTHERWISE, ARISING FROM, OUT OF OR IN CONNECTION WITH THE SOFTWARE OR THE USE OR OTHER DEALINGS IN THE SOFTWARE.
Sunday, March 28, 2010
Regression & Curve Fitting in Python – pt 1

Background
There are several good tutorials on linear regression and curve fitting using python already available. See here, here, here, and here. There is a quick note on curve fitting using genetic algorithms here. There is even an interesting foray into Bayesian Logistic Regression here. For simple regression problems involving only polynomials, look at the polyfit function. For other regression problems, the curve_fit function in scipy is available.This sequence of tutorials will introduce a less common approach to linear regression based on convex optimization. An excellent text on this topic, (although very dense reading) is Convex Optimization.
These tutorials show
- how to scale a set of functions to best approximate a set of data: curve fitting, regression, approximation, smoothing, interpolation, and extrapolation;
- what are the conditions for that fit to be best;
- how to use different functions like sine, cos, tan, log, and exp to find an analytic expression that ‘best’ describes arbitrary data; and
- how to use knowledge about the final function to improve a fit: monotonicity, convexity, extreme values, and limits.
Introduction
Lets start with a picture. This graph shows a trajectory fit to noisy data. Measurements on the trajectory are shown as red crosses and the regressed trajectory is shown as the black line. By the last entry of this tutorial, solving this kind of problem will be easy with a few lines of python.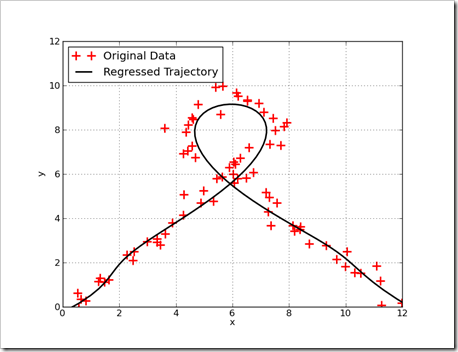
The Basics – Linear Regression using Polynomials
The usual regression question is how to fit a polynomial to a set of data. There is more to this question than appears at first. Fitting data involves answering the question of what is ‘best’. Linear regression answers that question by providing an answer that minimizes the sum if squares of difference between the fit and the data. This answer is useful in many cases, but not always! There are other answers.When fitting data to a polynomial, regression minimizes this expression:
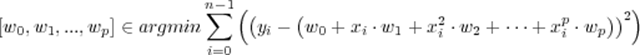
In this expression, xi and yi, are a data tuple and wi is the weighting to apply to each power of xi . The wi values are selected to minimize the squared difference between the estimate, which is a function of x, and the measurement y. This expression is used because it is easy to solve (once you know how), and it describes the maximum likelihood answer if the polynomial describes the relations between x and y (e.g. if there were no errors, the equations perfectly describe what is happening), the measurement errors are not correlated (e.g. independent and identically distributed – iid) and the errors have a zero mean gaussian distribution. Even when this is not the case, this approach is pretty good.
This equation can be solved in many ways with readily available software packages. In the Numpy libraries there is polyfit. Numpy also has lstsq, which solves a least squares fit. Argonne National Labs has a least squares fit package here that can find the best polynomial (or other families of functions). For this tutorial, things will be solved the hard way before existing libraries are used.
If the value for y are formed into a vector, and a special matrix, known as the Vandermonde matrix, is formed from the values of x, then the result is a linear system of equations.
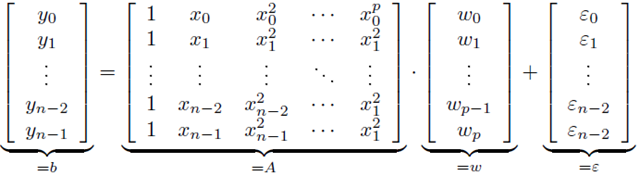 This matrix can be formed using the vander function in Numpy.For a fitting problem is in this form, it can be neatly expressed using matrix notation.
This matrix can be formed using the vander function in Numpy.For a fitting problem is in this form, it can be neatly expressed using matrix notation.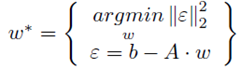 This can be solved numerically using an optimizer in scipy like fmin_slqp. This can be a very computationally expensive way to solve the problem (e.g. it takes a long time to solve). A more computationally efficiency (e.g. faster) way to solve this problem is to use the KKT conditions. This not only works, but results in the global optimum, because this problem is convex. This is important, because not all problems can easily be solved for the global optimum. Some problems have many local optimums, which make it difficult to find the best overall answer. Using the KKT conditions, the optimum values for w* are found using simple matrix operations.
This can be solved numerically using an optimizer in scipy like fmin_slqp. This can be a very computationally expensive way to solve the problem (e.g. it takes a long time to solve). A more computationally efficiency (e.g. faster) way to solve this problem is to use the KKT conditions. This not only works, but results in the global optimum, because this problem is convex. This is important, because not all problems can easily be solved for the global optimum. Some problems have many local optimums, which make it difficult to find the best overall answer. Using the KKT conditions, the optimum values for w* are found using simple matrix operations.A first example, the hard way…
Before fitting a curve to data, it helps to have data. The following python script will data for a quadratic relationship between x and y. The measurements of y will be corrupted by a Gaussian (or normal) noise. This model is expressed aswith the random noise described by
This python script will build a useful data set.
from pylab import * from random import normalvariate a = 0.03 b = –0.21 c = 0.4 f = lambda x,a=a,b=b,c=c:a*x**2+b*x+c xList = arange(-10,10,0.25) yListTrue = [f(x) for x in xList] yListMeasured = [y+normalvariate(0,1) for y in yListTrue]This script takes the lists of points and finds the best quadratic fit for the data.
# fit the data
def polyFit(xList,yList,order=1):
'''fit the data using a least squares and polynomial'''
fList = [(lambda x,n=n: x**n) for n in range(order,-1,-1)]
# build row for each element in y
bList = []
A_List = []
for (thisX,thisY) in zip(xList,yList):
bList.append(thisY)
A_Row = [f(thisX) for f in fList]
A_List.append(A_Row)
b = matrix(bList).T
A = matrix(A_List)
w = inv(A.T*A)*A.T*b
return w.T.tolist()[0]
w = polyFit(xList,yListMeasured,order=2)
aHat = w[0]
bHat = w[1]
cHat = w[2]
# summarize the results
print 'Data model is :%4.2f*x^2 + %4.2f*x + %4.2f' % (a,b,c)
print 'Fit equation is :%4.2f*x^2 + %4.2f*x + %4.2f' % (aHat,bHat,cHat)
# plot, for visual comparison
def getPolyF(w):
'''create a function using the fit values'''
return lambda x,w=w: sum([thisW*(x**(len(w)-n-1))
for n,thisW in enumerate(w)])
fHat = getPolyF(w)
xPlotList = arange(-10,10,0.1)
yEstList = [fHat(x) for x in xPlotList]
fTrue = getPolyF([a,b,c])
yTrueList = [fTrue(x) for x in xPlotList]
figure(1)
plot(xPlotList,yEstList,'--g',linewidth=2)
plot(xPlotList,yTrueList,'b',linewidth=2)
plot(xList,yListMeasured,'+r',markersize = 12,markeredgewidth=2)
xlabel('x')
ylabel('y')
legend(['estimate','true','measured'])
grid(True)
savefig('secondOrderFitEx.png')
show()When this script is run, the console output isDifferent answers will occurs on each run because random numbers are used.Data model is :0.03*x^2 + -0.21*x + 0.40 Fit equation is :0.03*x^2 + -0.26*x + 0.46
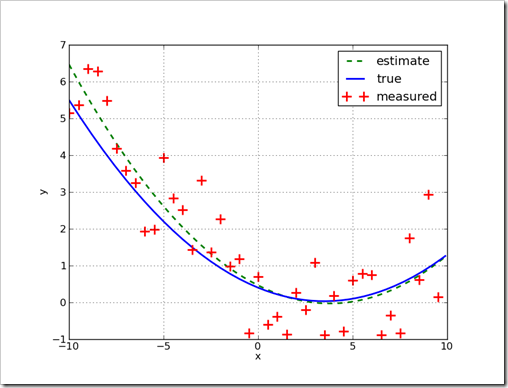
Another example, simpler this time…
In the first example, a lot of the code was built by hand. To make the task easier, the libraries in Numpy & Scipy are used.The first change is to incorporate the vander function and psuedo inverse, pinv, functions into the polyFit function. The vander function builds the Vendermonde matrix and the pinv function performs the same operation as inv(A.T*A)*A.T
def polyFit(xList,yList,order=1):
'''fit the data using a least squares and polynomial'''
A = vander(xList,order+1)
b = matrix(yList).T
w = pinv(A)*b
return w.T.tolist()[0]Alternatively, the polyFit function could be created using the lstsq function. This function is nice because it provides additional information that can be useful in checking on the quality of a fit.def polyFit(xList,yList,order=1):
'''fit the data using a least squares and polynomial'''
A = vander(xList,order+1)
b = matrix(yList).T
(w,residuals,rank,sing_vals) = lstsq(A,b)
return w.T.tolist()[0]Finally, the polyFit function could be eliminated entirely, and replaced with the polyfit function. The second change is to replace the getPolyF function with the poly1d function in Numpy. This gets rid of a few lines of code.
fHat = poly1d((aHat,bHat,cHat)) xPlotList = arange(-10,10,0.1) yEstList = [fHat(x) for x in xPlotList] fTrue = poly1d((a,b,c)) yTrueList = [fTrue(x) for x in xPlotList]Combining all of these changes, the example script becomes….
from pylab import *
from random import normalvariate
# generate the data
a = 0.03
b = -0.21
c = 0.4
f = lambda x,a=a,b=b,c=c:a*x**2+b*x+c
xList = arange(-10,10,0.5)
yListTrue = [f(x) for x in xList]
yListMeasured = [y+normalvariate(0,1) for y in yListTrue]
# fit the data
w = polyfit(xList,yListMeasured,2)
aHat = w[0]
bHat = w[1]
cHat = w[2]
# summarize the results
print 'Data model is :%4.2f*x^2 + %4.2f*x + %4.2f' % (a,b,c)
print 'Fit equation is :%4.2f*x^2 + %4.2f*x + %4.2f' % (aHat,bHat,cHat)
# plot, for visual comparison
fHat = poly1d((aHat,bHat,cHat))
xPlotList = arange(-10,10,0.1)
yEstList = [fHat(x) for x in xPlotList]
fTrue = poly1d((a,b,c))
yTrueList = [fTrue(x) for x in xPlotList]
figure(1)
plot(xPlotList,yEstList,'--g',linewidth=2)
plot(xPlotList,yTrueList,'b',linewidth=2)
plot(xList,yListMeasured,'+r',markersize = 12,markeredgewidth=2)
xlabel('x')
ylabel('y')
legend(['estimate','true','measured'])
grid(True)
savefig('secondOrderFitEx.png')
show()The real work for fitting the polynomial is now done by one line of code, and the reconstruction of the curve is done by another.The reason for performing the fits using custom code is so later, more interesting fits can be found.
See part 2 for a tutorial on weighted fitting & regression.
All text is copyright © 2010, Ed Tate, All Rights Reserved.
All software and example codes are subject to the MIT License
Copyright (c) 2010, Ed Tate, Permission is hereby granted, free of charge, to any person obtaining a copy of this software and associated documentation files (the "Software"), to deal in the Software without restriction, including without limitation the rights to use, copy, modify, merge, publish, distribute, sublicense, and/or sell copies of the Software, and to permit persons to whom the Software is furnished to do so, subject to the following conditions: The above copyright notice and this permission notice shall be included in all copies or substantial portions of the Software.
THE SOFTWARE IS PROVIDED "AS IS", WITHOUT WARRANTY OF ANY KIND, EXPRESS OR IMPLIED, INCLUDING BUT NOT LIMITED TO THE WARRANTIES OF MERCHANTABILITY, FITNESS FOR A PARTICULAR PURPOSE AND NONINFRINGEMENT. IN NO EVENT SHALL THE AUTHORS OR COPYRIGHT HOLDERS BE LIABLE FOR ANY CLAIM, DAMAGES OR OTHER LIABILITY, WHETHER IN AN ACTION OF CONTRACT, TORT OR OTHERWISE, ARISING FROM, OUT OF OR IN CONNECTION WITH THE SOFTWARE OR THE USE OR OTHER DEALINGS IN THE SOFTWARE.